The law of one price: similar things must have similar prices
Replication: the only reliable way to value a security
A simple up-down model for the risk of stocks, in which expected return \(\mu\) and volatility \(\sigma\) are all that matter
The Law of one price leads to CAPM for stocks
Replicating derivatives via the law of one price

Replication

replication의 아이디어는 이미 가격을 알고 있는 비슷한 financial instruments로 가격을 모르는 상품의 가격을 알고자 하는 것

The one law of quantitative finance

If 2 securities have identical payoffs under all possible future scenarios, then the 2 securities should have identical current prices

It should be impossible to obtain for zero cost a security that has non-negative payoffs in all future scenarios, with at least 1 scenario having a positive payoff

In the long run, in liquid markets, the law of one price usually holds. In practice, in the short run, in illiquid markets or during financial crises and panics, the law of one price may not hold.

Valuation by replication

To estimate the unknown value of a target security, find some replicating portfolio, a set of more liquid securities with known prices, that has the same payoffs as the target, no matter how the future turns out.

To demonstrate the target and the replicating portfolio have identical future payoffs under all circumstances.

specify what you mean by ‘under all circumstances’ for each security
find a strategy for creating a replicating portfolio that, in each future scenario or circumstance

We must create a replicating portfolio of liquid securities whose payoffs match the payoffs of the target in all future scenarios.

Styles of replication

Static replication

When finish construction of replicating portfolio, no need additional trading required for the lifetime of the target security

Dynamic replication

The components and weights of replicating portfolio must change over time
Need to continually trade as time passes and the prices of the underlying securities in order to maintain the replication

1973년 Black-Scholes equation은 option의 dynamic replication을 가능하게 해준 일대의 사건

The limits of replication

All financial models are based on assumptions

At best, therefore, financial models are only approximations to reality. Understanding the assumptions of financial models is the key to understanding the limits of replication.

replication steps

Capture the reality as much as possible
Determining weights matters at all, in theory in replication
1. In reality, adjusting weights by trading is problematic - bid-ask spread, market impact, financing costs, transaction costs, operational risks, impossible-to-observed variables (ex. future volatility)

In actual markets, replicating strategy is rarely found. Economic model can be the alternatives. However, it is a matter of how people feel. So that, utility functions underlying the economic model are the hidden variables of economic theory, quantities never directly observed.

Modeling the risk of underliers

modeling은 underliers의 behavior를 나타내는 것으로 시작

modern portfolio theory는 efficient market hypothesis에 기반을 두고 있는데, 이는 2007-2008년 금융위기를 기점으로 비판을 받고 있음

The efficient market hypothesis

1960년대 University of Chicago를 위시로 한 Eugene Fama는 Efficient market hypothesis를 발표

이는 이후 몇년간 수학적인 발전을 이뤄 종국에는 strong, weak 등과 같은 efficiency의 정도를 구분하는 것으로 정리되었다.

EMH는 장기적으로 시장을 이기는 것은 불가능하고, 이는 현재의 모든 경제와 시장의 정보가 가격에 반영되어있기 때문이라고 주장했다. 이는 systmetic하게 가격을 예측하는 것이 불가능하니 이를 가설로 만들어 버린 것으로도 볼 수 있다.

Uncertainty, risk, and return

Risk is quantifiable but uncertainty is not quantifiable.

The risk of stocks

The most important feature of a stock is the uncertainty of its returns.

The volatility is a measure of the stock’s risk.

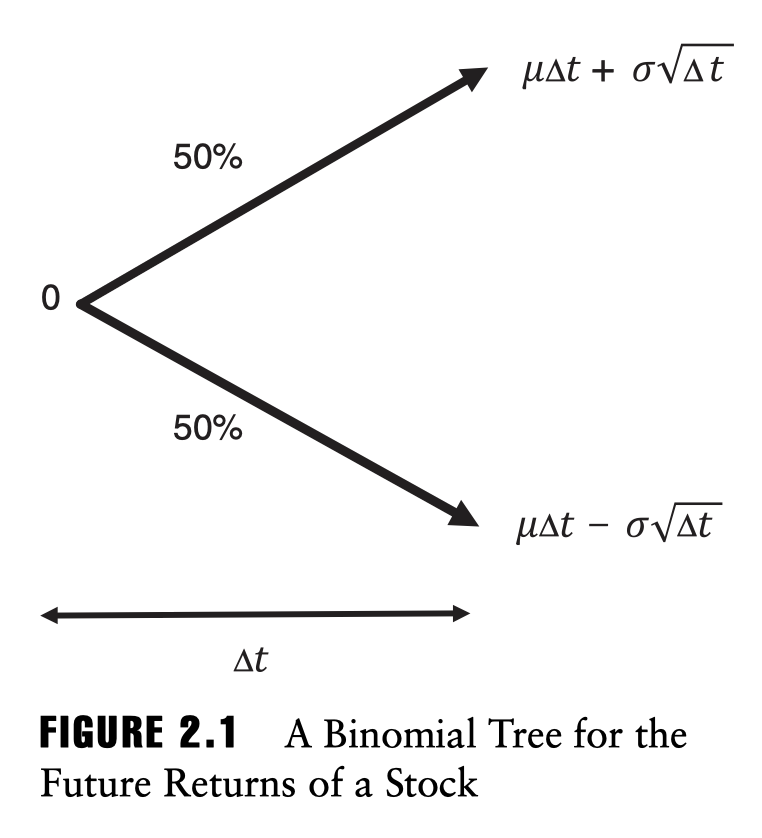
Binomial model의 특징은 expected return과 volatility로 주가의 움직임을 타나낸다는 점인데, 이는 굉장히 강한 가정임에 틀림없다. 그러나 the law of one price와 결부되어 CAPM, Black-Scholes-Merton option pricing formula까지 발전한다.

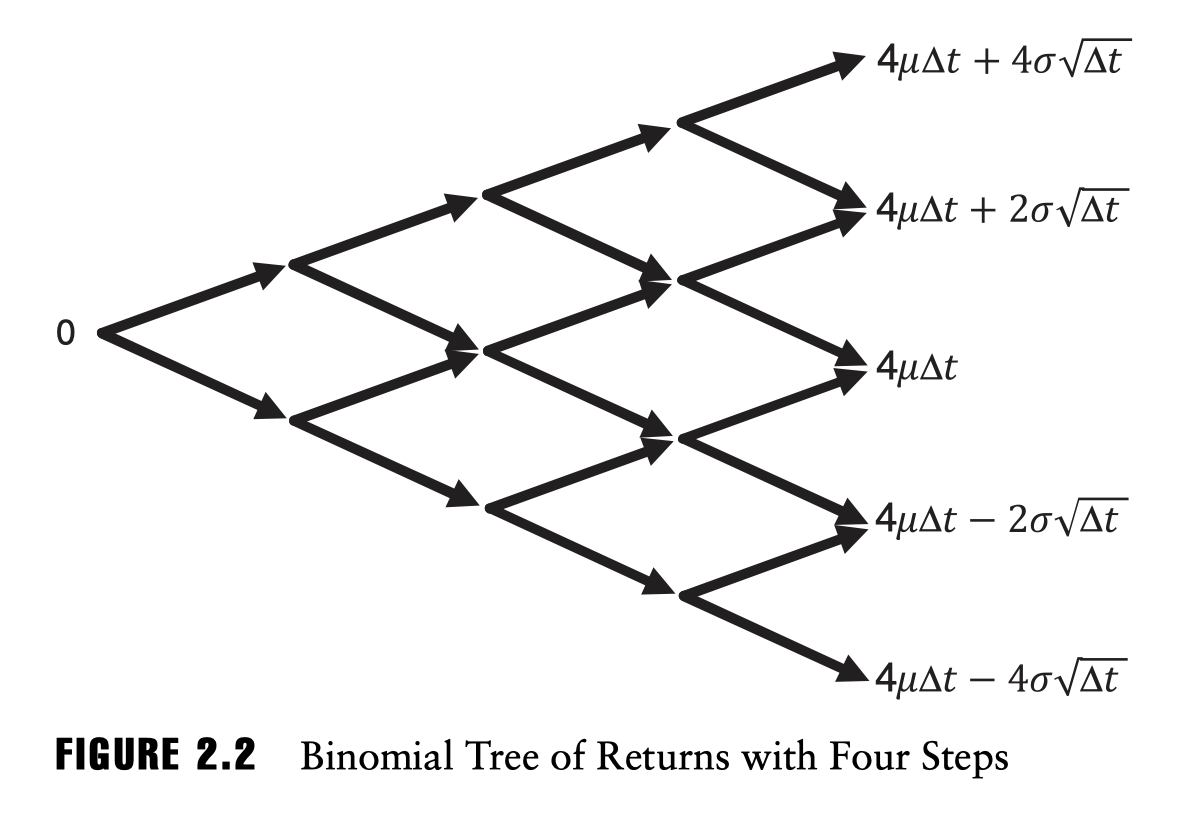
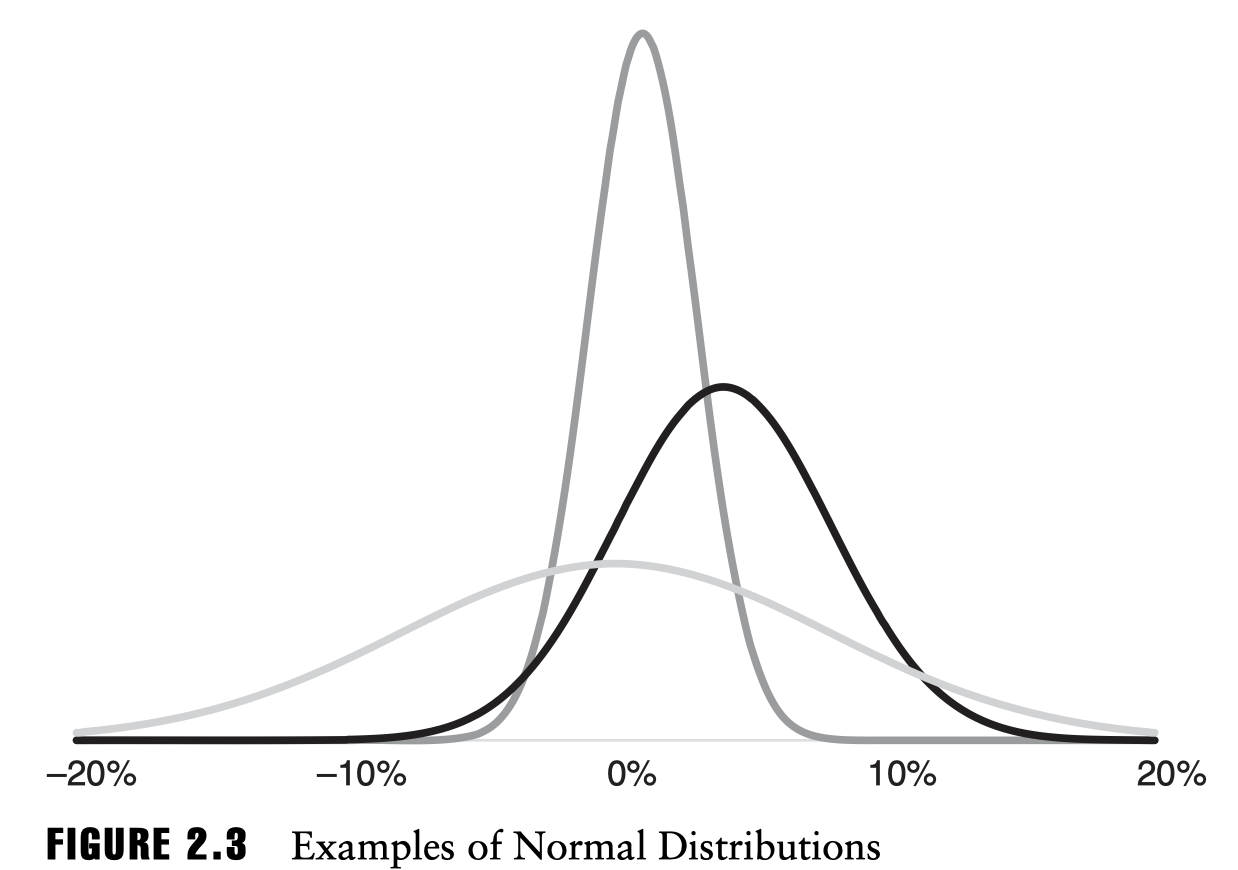
아주 간단한 모델에서는 symmetric distribution을 사용하는데 이는 일반적으로 negative skewness를 가지는 주가 수익률의 분포와는 다소 거리가 있다. ex) fat tail

그러나 symmetric distribution은 modeling을 배우기에 아주 좋은 시작점이다. 실제 주가의 움직임은 굉장히 복잡하고 예측불가능하지만, binomial model은 직관적으로 쉬운 접근법을 제시한다.

Riskless bonds

The riskless rate is ubiquitous throughout economics and finance and is central to the replication and valuation of options.

riskless bond의 binomial tree를 그리면 가격은 up과 down 사이에 넣이게 될텐데, 그 어떤 경우에라도 riskless이기 때문에 positive payoff를 나타내는 모순이 발생한다. - 솔직히 이거 왜 설명하는지 모르겠지만

In the reality, the US treasury bill is commonly considered as a riskless rate.

Key question of investing

What anticipated possible future reward justifies a particular anticipated risk?

The law of one price states that securities with identical payoffs under all possible circumstances should have identical prices.

With in the binomial framework

What is the relation between expected return and volatility?

Some investment risks can be avoided

The law of one price says that the securities with identical risk should have identical expected returns

There are 2 types of risk

avoidable risk - by diversification, dilution, or hedging
unavoidable risk

So that, the law of one price is restated as

Identical unavoidable risks should have identical expected returns

Assumptions

It has the same return as other unavoidable risks of the same size
The principle of replication applies to it and all other securities

The results we deduce in those worlds will logically consistent, but will not resemble the relation between expected return and volatility in actual market.

World #1: only a few uncorrelated stocks and a riskless bond

uncorrelated stock과 riskless bond만 존재하는 세상

다르게 말하면 stock이 유일한 unavoidable risk를 가짐

모두 uncorrelated 되어있기 때문에 hedging이나 diversification으로 risk hedge가 불가능

riskless와의 조합으로 risk를 줄일 수 있음

\[ \mu_P = w\mu + (1 - w)r = r + w(\mu - r) \]

\[ \lambda_P \equiv \frac{\mu_P - r}{\sigma_P} = \frac{w(\mu - r)}{w\sigma} = \lambda \equiv \frac{\mu - r}{\sigma} \]

\(\lambda\)는 1966년 William Sharpe가 만든 Sharpe ratio로 excess return earned per unit of risk를 의미한다.

포트폴리오의 Sharpe ratio는 오로지 주식의 expected return과 volatility로만 결정되며, 모든 stock은 uncorrelated 되어 있으므로 모든 주식에 대해서도 똑같이 적용할 수 있다.

이는 more unavoidable risk, more expected return을 reconfirm 해준다고 볼 수 있다.

참고로 Sharpe ratio는 시계열 개념없이 보통 연율화된 수치로 계산을 많이 하는데, 이는 시점을 조절하면 결과 값이 바뀌는 것을 의미한다.

In the World #1, the law of one price는 the same for all uncorrelated securities.

World #2: an infinite number of uncorrelated stocks and a riskless bond

Diversification is a basic strategy to reduce risks. However, in the World #2, diversification with an infinite number of uncorrelated stocks having a same volatility is same to the return of riskless bond.x

\[ \lim_{n \to \infty}\frac{\mu_P - r}{\sigma \sqrt{n}} \]

All the risks are removed and then the portfolio’s risk is same as the risk of riskless bond. Then, the Sharpe ratio is zero for all the stocks in this model world.

World #3: an infinite number of stocks all simultaneously correlated with the entire market, and a riskless bond

In the reality, we cannot remove the risks from diversification.

Equity는 same macroeconomic factor들에 의해 driven → diversification을 해버리면 risk를 modest level까지 줄일 수 있지만, market risk는 줄이지 못함

World #3에서는 market factor인 M이 모든 stock에 영향을 주기 때문에, 각 stock의 market-related 부분을 헷지해서 없애버리면서 market-neutral stock으로 구성된 포트폴리오를 만든다. 이렇게 구성하면 diversification으로 개별 stock의 risk는 제거되고, 마찬가지로 market-neutral hedge를 해버려서 market risk도 제거된다. 초과수익이 없는 완전 무위험 포트폴리오가 탄생하고 이는 CAPM의 결론에 비슷하게 도달한다.

\[ \Delta_i = \rho_i \frac{\sigma_i}{\sigma_M}\frac{S_i}{M} = \beta_i\frac{S_i}{M} \]

market-neutral version of the ith stock

\[ \tilde S_i = S_i - \Delta_i M \]

\[ \tilde \mu_i = \frac{\mu_i - \beta_i \mu_M}{1 - \beta_i} \]

\[ \mu_i S_i - \beta_i \frac{S_i}{M}M \mu_M = (\mu_i - \beta_i \mu_M) S_i \]

\[ S_i - \Delta_i M = S_i - \beta_i \frac{S_i}{M}M = (1 - \beta_i)S_i \]

\[ \mu_i - r = \beta_i (\mu_M - r) \]

This result is known as the Sharpe-Lintner-Mossin capital asset pricing model, later genearlized to the arbitrage pricing theory by Stephen Ross. It states that, if all that matters to investors is \(\mu\) and \(\sigma\), and equal unavoidable risks lead to equal expected returns, then the excess return you can expect from buying a stock is \(\beta\) times the expected excess return of every stock’s common hedgeable factor, in this case the market. You can only expect to be rewarded for the unavoidable factor risk of each stock, because all other risks can be eliminated by hedging.

Derivatives are not independent securities

A derivative is a contract

abhor

regard with disgust and hatred