
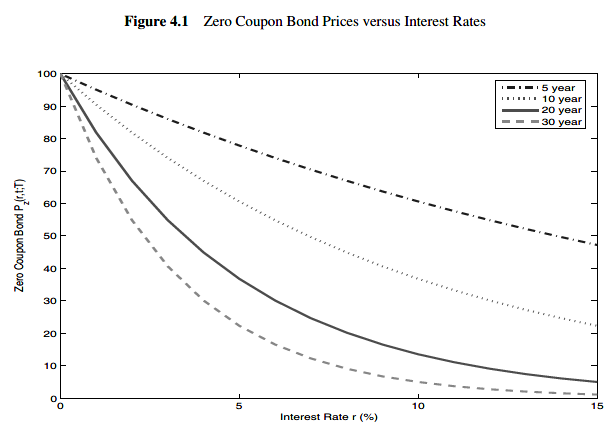
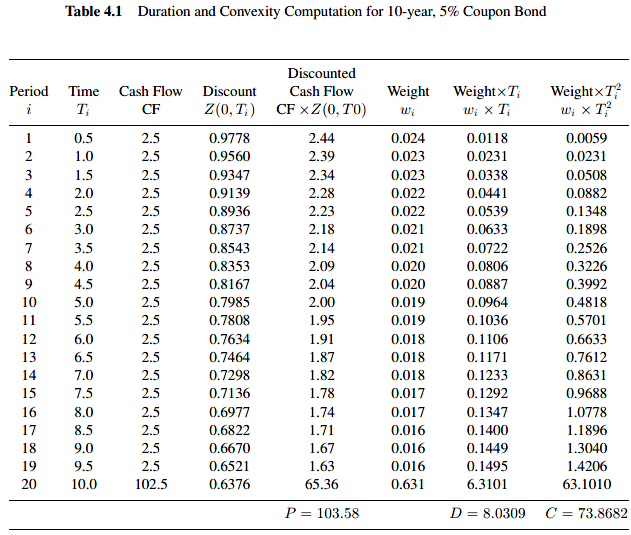
The relation between bond prices and interest rates is not linear.
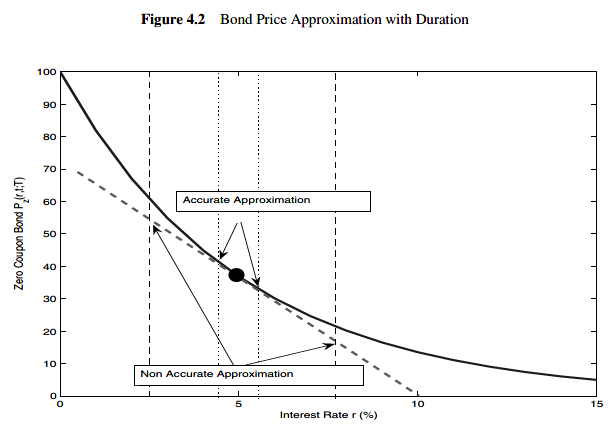
Clearly, for small changes in interest rate, the straight line and the curved line are very close to each other. However, for large changes, the approximation is relatively poor.
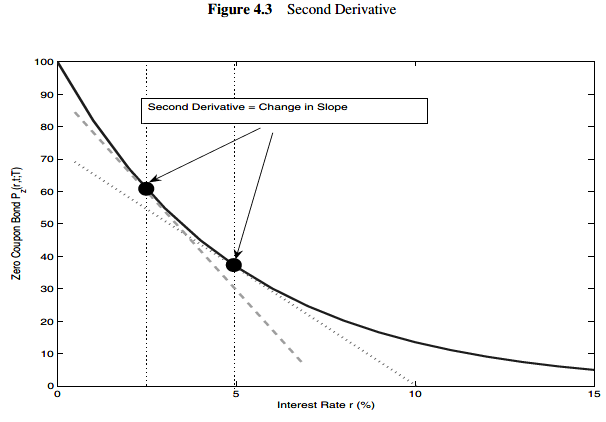
To obtain a more accurate measure of the impact that a change in the term structure has on bond prices, we must take into account the convexity of the bond with respect to interest rate. The convexity can be measured by referring to the notion of second derivative.
The second derivative of a function F(x), denoted by
The curvature of the function is effectively measured by the change in slope.
The convexity of a security with price P measures the percentage change in the price of the security due to the curvature of the price with respect to the interest rate r. Formally
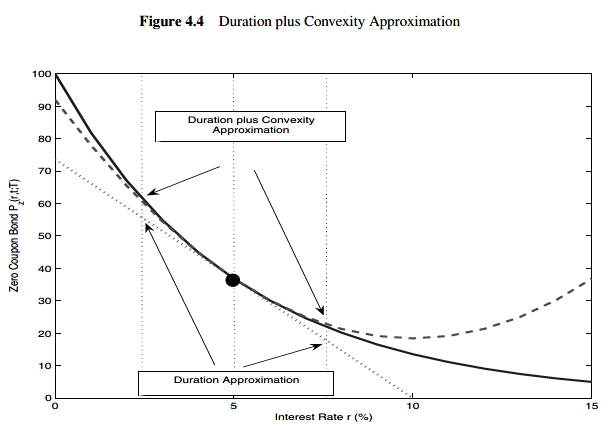
An approximation of the percentage impact of interest rates on the price of a security is given by
In other words, the convexity term C arguments the precision of the approximation made by the duration term, but it does not substitute for it.
The convexity of zero coupon bonds
The convexity of the zero coupon bond is
The convexity of a portfolio of securities
The convexity of a coupon bond

Positive convexity: good news for average returns
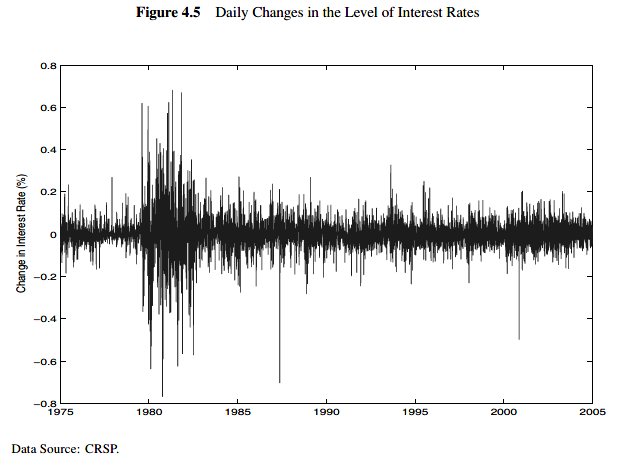
In statistics, when E[dr] = 0 this quantity corresponds to the variance of the change in level of interest rates. That is, it measures the size of daily fluctuations in interest rates. The key insight is that although we do not know the direction in which the interest rate will move between today and tomorrow, it is extremely likely it will move. That is, the variance of interest rates is positive,
A common pitfall
A common pitfall is to think of ‘convexity’ as the ‘change in duration’
The correct statement is instead that the curvature of a function, represented by its second derivative, is indeed equal to the change in slope of the function, given by the first derivative.
In this case, indeed, the dollar convexity is related to the change in dollar duration. In particular, by the definition of second derivative, the dollar convexity equals the change of the negative of the dollar duration.
Convexity and risk management
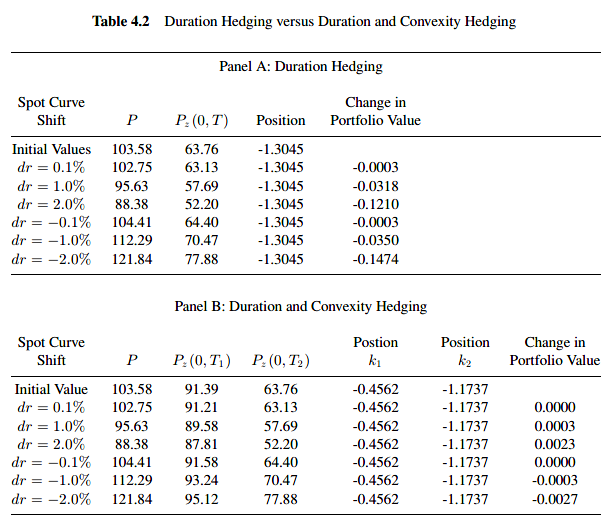
Taking into account convexity improves the performance of interest rate risk management practices, especially in an environment with substantial shifts in the yield curve.
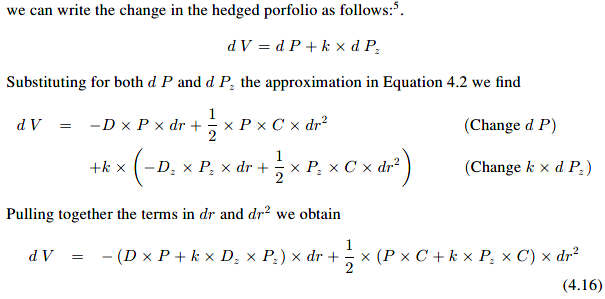

Convexity trading and the passage of time
If w e go long bond with high convexity, such as long-term bonds, and duration hedge the interest rate risk using bonds with low convexity, such as short-term bonds, we gain positive returns from convexity.
A barbell bond position consists of a portfolio that is long both high duration and low duration assets, while a bullet bond position is a position long a medium duration asset. The strategy then consists in going long a barbell position, and hedging it with a bullet position, with the same duration. Such a strategy results in a positive convexity strategy.
The question is then whether the convexity trading strategy represents an arbitrage opportunity. The answer is no. The reason is that the duration hedging argument leaves out an important dimension of bond return, and this is time.
From these models that the convexity trading strategy has an important drawback, and this is the fact that the gain in value from higher convexity is offset by a lower gain due to the passage of time, a relation that is known as the Theta-Gamma relation.