- the derivation of the Black-Scholes formulae for calls, puts and simple digitals
- the meaning and importance of the ‘greeks,’ delta, gamma, theta, vega and rho
- the difference between differentiation with respect to variable and to parameters
- formulae for the greeks for calls, puts and simple digitals
Introduction
Other derivatives of the option price are important in the hedging of an option position, playing key roles in risk management. It can be argued that it is more important to get the hedging correct than to be precise in the pricing of a contract.
Derivation of the formulae for calls, puts and simple digitals
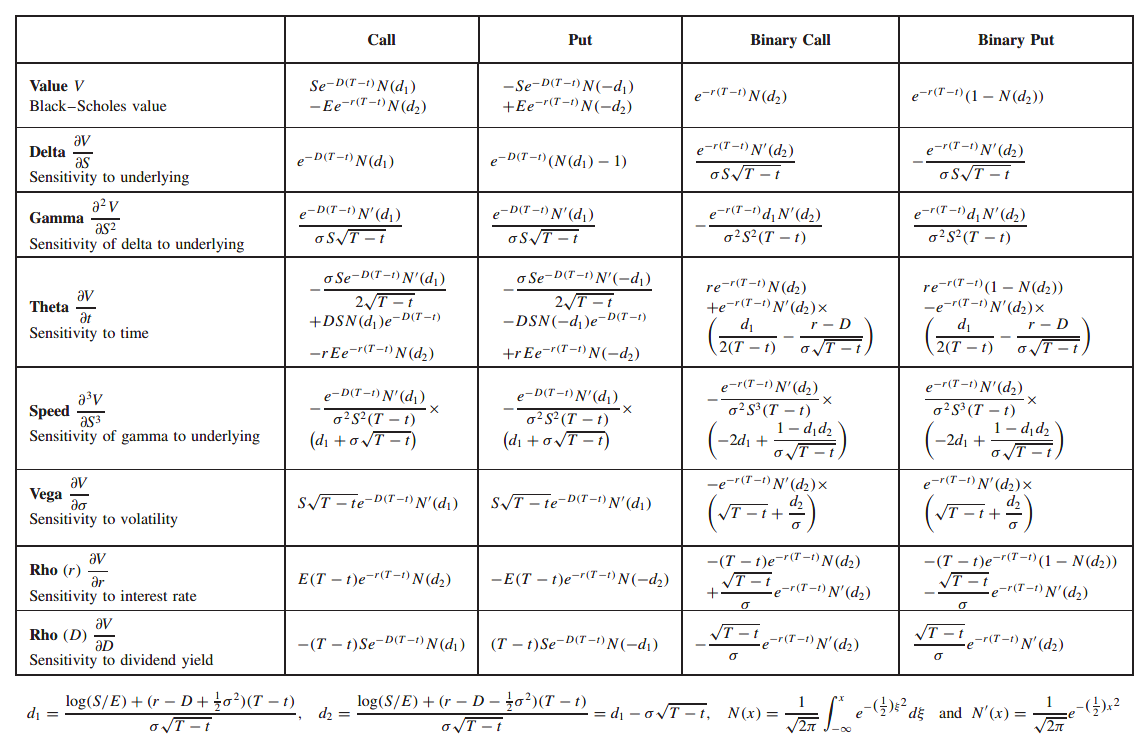
The Black-Scholes equation is
\[ \frac{\partial V}{\partial t} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 \]
This equation must be solved with final condition depending on the payoff; each contract will have a different functional form prescribed at expiry t = T. This is the final condition that must be imposed to make the solution unique.
The first step in the manipulation is to change from present value to future value terms. Recalling that the payoff is received at time T but that we are valuing the option at time t this suggests that we write
\[ V(S, t) = e^{-r(T - t)}U(S, t) \]
\[ \frac{\partial U}{\partial t} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 U}{\partial S^2} + rS \frac{\partial U}{\partial S}= 0 \]
\[ \tau = T - t \]
\[ \frac{\partial U}{\partial \tau} = \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 U}{\partial S^2} + rS \frac{\partial U}{\partial S} \]
Why is rV removed in the Black-Scholes equation for futures comparing to equity?
When we first started modeling equity prices we used intuition about the asset price return to build up the stochastic differential equation model.
\[ \xi = \log{S} \]
\[ \frac{\partial}{\partial S} = e^{-\xi}\frac{\partial}{\partial \xi} ~ and ~ \frac{\partial^2}{\partial S^2} = e^{-2\xi}\frac{\partial^2}{\partial \xi^2} - e^{-2\xi}\frac{\partial}{\partial \xi} \]
\[ \frac{\partial U}{\partial \tau} = \frac{1}{2} \sigma^2 \frac{\partial^2 U}{\partial \xi^2} + (r - \frac{1}{2}\sigma^2) \frac{\partial U}{\partial \xi} \]
It has taken the problem defined for \(0 \leq S < \infty\) to one defined for \(-\infty < \xi < \infty\). But more importantly, the coefficients in the equation are now all constant, independent of the underlying.
\[ x = \xi + (r + \frac{1}{2}\sigma^2)\tau \]
\[ U = W(x, \tau) \]
This is just a ‘translation’ of the coordination system. It’s a bit like using the forward price of the asset instead of the spot price as a variable. After this change of variables the Black-Scholes becomes the cimpler
\[ \frac{\partial W}{\partial \tau} = \frac{1}{2}\sigma^2\frac{\partial^2 W}{\partial x^2} \]
\[ V(S, t) = e^{-r(T - t)}U(S, t) = e^{-r\tau}U(S, T - \tau) = e^{-r\tau}U(e^\xi, T - \tau) = e^{-r\tau}U\left(e^{x - (r - \frac{1}{2}\sigma^2)\tau)}, T - \tau \right) = e^{-r\tau}W(x, \tau) \]
\[ x = \xi + (r - \frac{1}{2}\sigma^2)\tau = \log{S} + (r - \frac{1}{2}\sigma^2)(T - t) \]
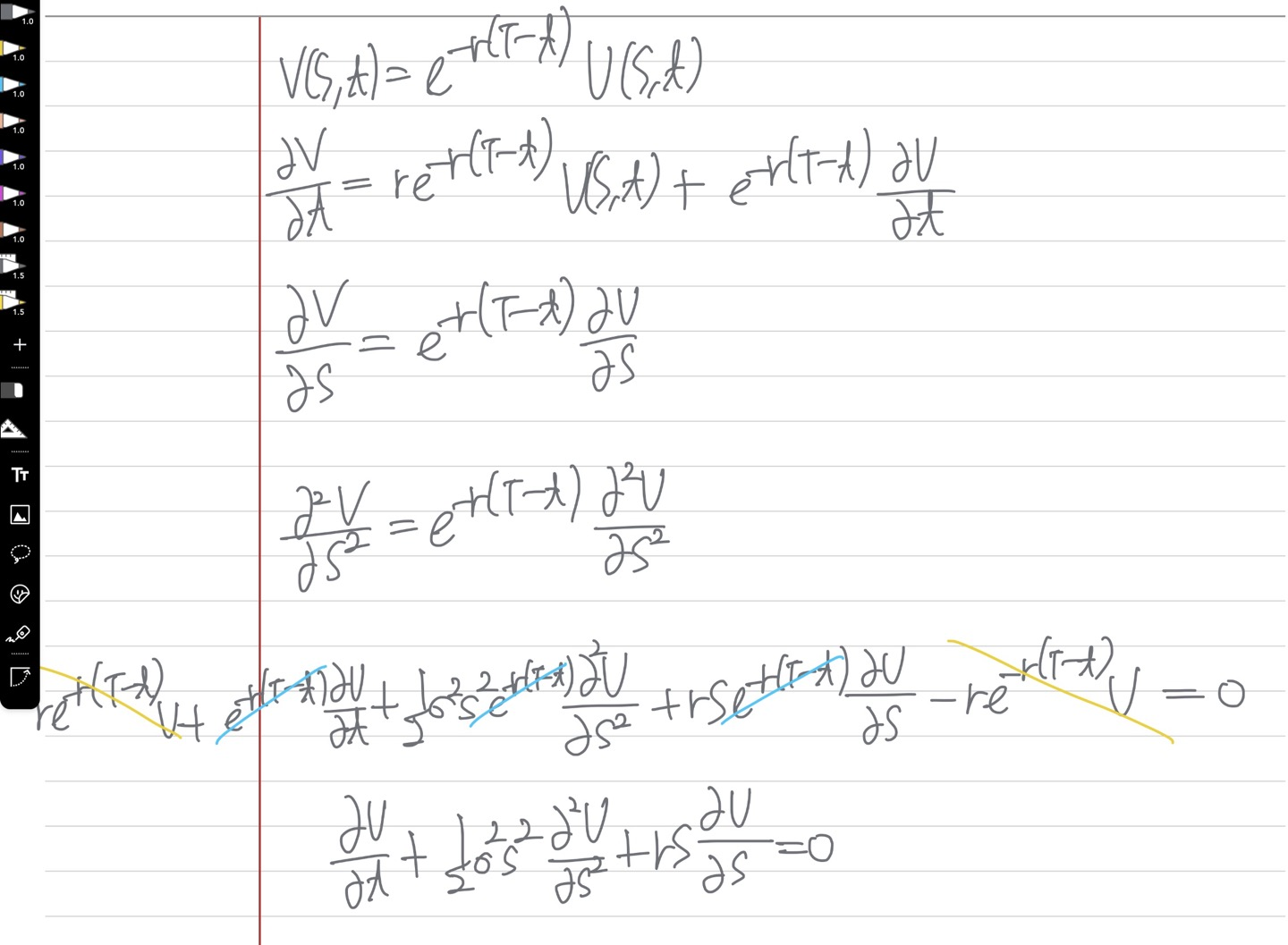
An expression for the value of any option whose payoff is a known function of the asset price at expiry. This includes calls, puts, and digitals. This expression will be in the form of an integral. For special cases, the integral is rewritten in terms of the cumulative distribution function of the normal distribution. But there are two steps before this integral.
The first step is to find a special solution called the fundamental solution. This solution has useful properties. The second step is to use the linearity of the equation and the useful properties of the special solution to find the general solution of the equation.
\[ W(x, \tau) = \tau^\alpha f\left(\frac{(x - x')}{\tau^\beta}\right) \]
where x’ is an arbitrary constant. This special solution is called \(W_f(x, \tau; x')\). Note that the unknown function depends on only one variable \((x - x')/\tau^\beta\). As well as finding the function f we must find the constant parameters \(\alpha\) and \(\beta\). We can expect that if this approach works, the equation for f will be an ordinary differential equation since the function only has one variable.
\[ \tau^{\alpha - 1}\left(\alpha f - \beta \eta\frac{df}{d\eta} \right) = \frac{1}{2}\sigma^2 \tau^{\alpha - 2\beta}\frac{d^2 f}{d \eta^2} \]
\[ \eta = \frac{x - x'}{\tau^\beta} \]
\[ \alpha - 1 = \alpha - 2\beta ~ i.e. ~ \beta = \frac{1}{2} \]
\[ \int_{-\infty}^\infty{\tau^\alpha f((x - x') / \tau^\beta)dx} \]
to be constant.
\[ \int_{-\infty}^\infty{\tau^{\alpha + \beta}f(\eta)d\eta} \]
\[ \alpha = -\beta = -\frac{1}{2} \]
\[ -f -\eta\frac{df}{d\eta} = \sigma^2 \frac{d^2 f}{d \eta^2} \]
\[ \sigma^2 \frac{d^2 f}{d \eta^2} + \frac{d(\eta f)}{d\eta} = 0 \]
\[ \sigma^2 \frac{df}{d\eta} + \eta f = a \]
where a is a constant. For the special solution, a = 0.
\[ f(\eta) = be^{-\eta^2 / (2 \sigma^2)} \]
the constant b such that the integral of f from minus infinity to plus infinity is one:
\[ f(\eta) = \frac{1}{\sqrt{2\pi \sigma}}e^{-\eta^2 / (2\sigma^2)} \]
\[ W_f(x, \tau) = \frac{1}{\sqrt{2 \pi \tau}\sigma}e^{-((x - x')^2 / 2\sigma^2 \tau)} \]
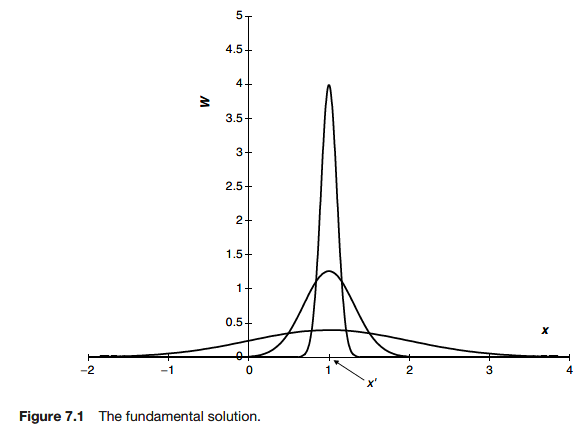
Although the function is increasingly confined to a narrower and narrower region its area remains fixed at one. These properties of decay away from one point, unbounded growth at that point and constant area, result in a Dirac delta function \(\delta(x' - x)\) as \(\tau \to 0\). The delta function has one important property, namely
\[ \int{\delta(x' - x)g(x')dx'} = g(x) \]
where the integration is from any point below x to any point above x. Thus the delta function ‘picks out’ the value of g at the point where the delta function is singular i.e. at x’ = x. In the limit as \(\tau \to 0\) the function \(W_f\) becomes a delta function at \(x = x'\). This means that
\[ \lim_{\tau \to 0}{\frac{1}{\sqrt{2\pi \tau}}}\int_{-\infty}^\infty{e^{-\frac{(x' - x)^2}{2 \sigma^2 \tau}}g(x')dx'} = g(x) \]
This property of the special solution, together with the linearity of the Black-Scholes equation, are all that are needed to find some explicit solutions.
\[ V(S, T) = Payoff(S) \]
\[ W(x, 0) = Payoff(e^x) \]
\[ W(x, \tau) = \int_{-\infty}^\infty{W_f(x, \tau; x')Payoff(e^{x'})dx'} \]
The integration with respect to x’ is similar to a summation, and since each individual component satisfies the equation so does the sum/integral.
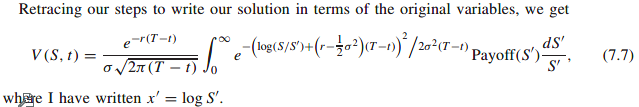
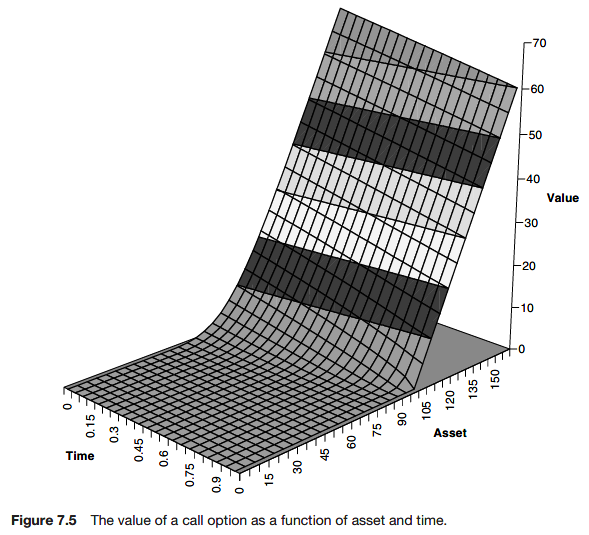
This is the exact solution for the option value in terms of the arbitrary payoff function.
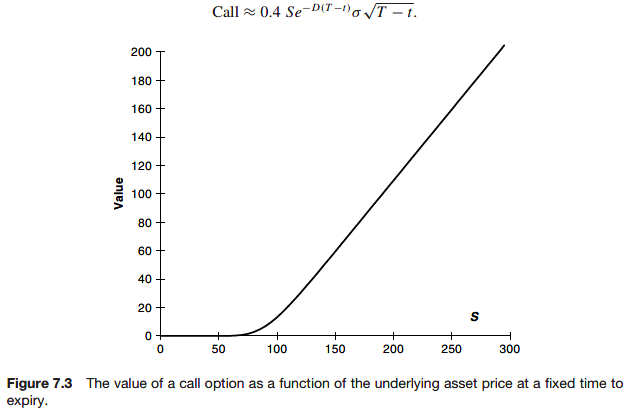
Formula for a call
\[ \text{Call option value} = SN(d_1) - e^{-r(T - t)}N(d_2) \]
\[ d_1 = \frac{\log{(S/E)} + (r + \frac{1}{2}\sigma^2)(T - t)}{\sigma \sqrt{T - t}} \]
\[ d_2 = \frac{\log{(S/E)} + (r - \frac{1}{2}\sigma^2)(T - t)}{\sigma \sqrt{T - t}} = d_1 - \sigma\sqrt{T - t} \]
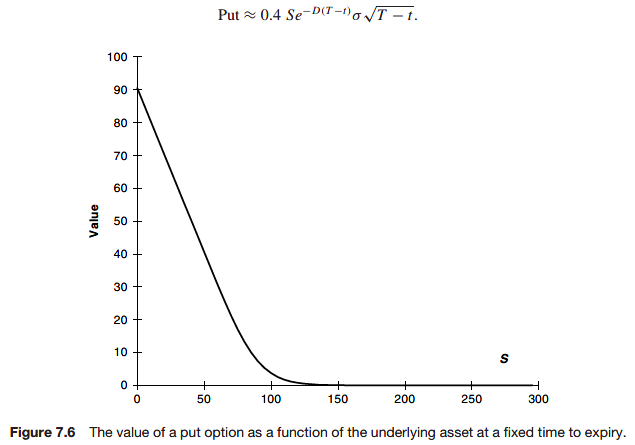
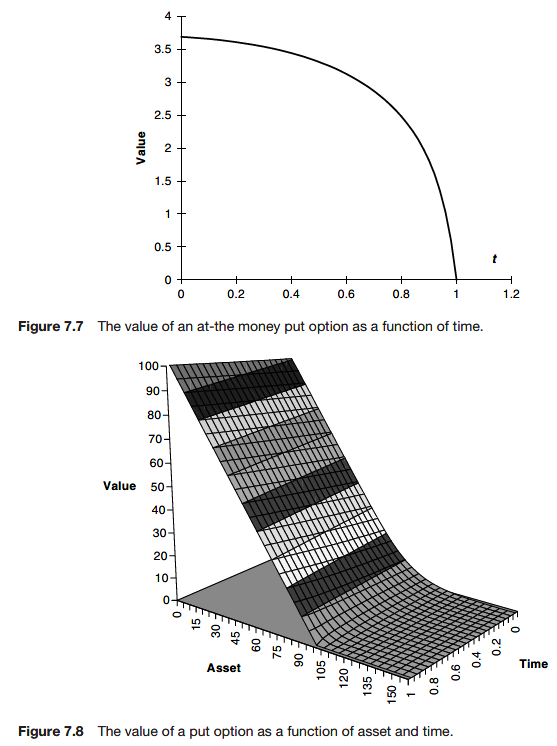
Formula for a put
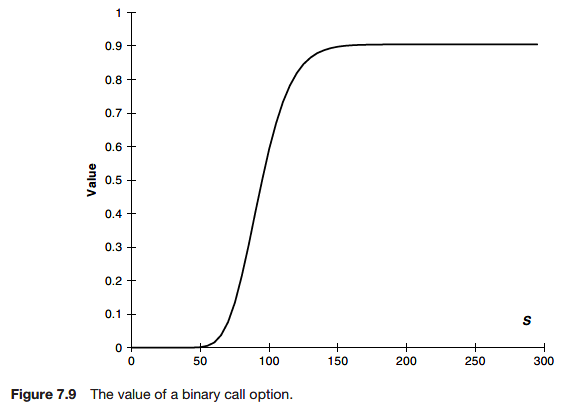
Formula for a binary call
Formula for a binary put
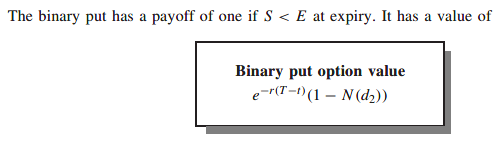
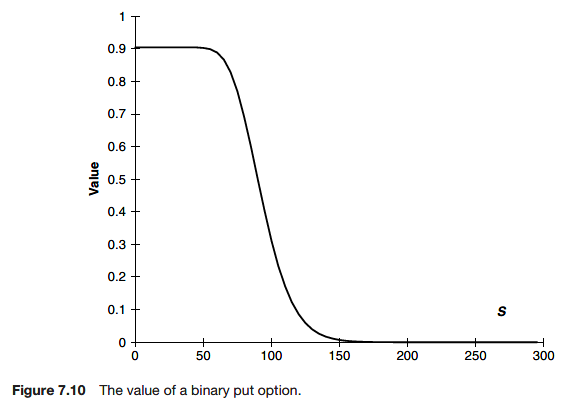
Delta
The delta of an option or a portfolio of options is the sensitivity of the option or portfolio to the underlying. It is the rate of change of value with respect to the asset
\[ \Delta = \frac{\partial V}{\partial S} \]
Here V can be the value of a single contract or of a whole portfolio of contracts. The delta of a portfolio of options is just the sum of the delta of all the individual positions.
Speculator
- only naked position held
- not hedge at all
Hedger
- hold a position already and want to eliminate some very specific risk
- selling (or buying) the options because they believe they have a better price and can make money by hedging away all risk → delta hedge
Delta hedging means holding one of the option and short a quantity \(\Delta\) of the underlying. This function varies as S and t vary. This means that the number of assets held must be continuously changed to maintain a delta-neutral position; this procedure is called dynamic hedging. Changing the number of assets held requires the continual purchase and/or sale of the stock. This is called rehedging or rebalancing the portfolio.
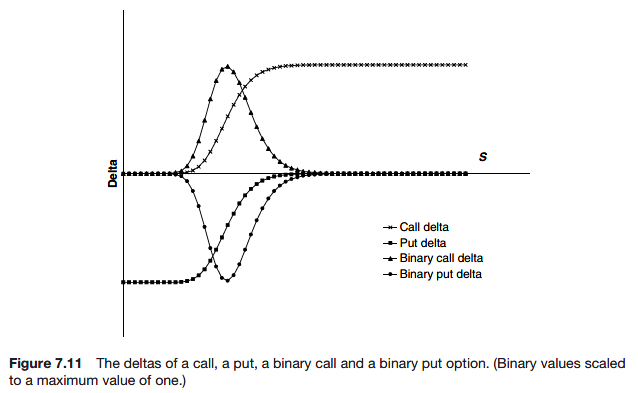
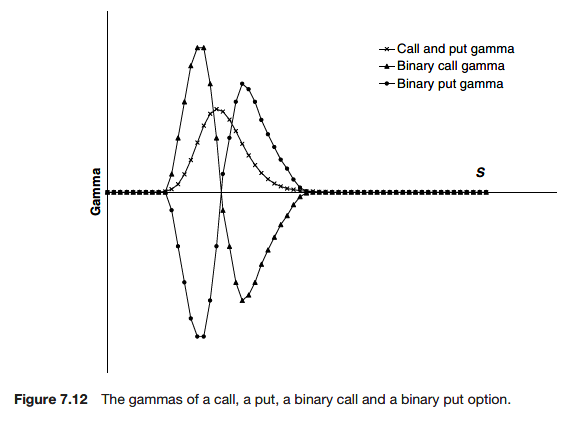
Gamma
The gamma of an option or a portfolio of options is the second derivative of the position with respect to the underlying
\[ \Gamma = \frac{\partial^2 V}{\partial S^2} \]
Since gamma is the sensitivity of the delta to the underlying it is a measure of by how much or how often a position must be rehedged in order to maintain a delta-neutral position. Although the delta also varies with the time this effect is dominated by the Brownian nature of the movement in the underlying.
In a delta-neutral position the gamma is partly responsible for making the return on the portfolio equal to the risk-free rate, the no-arbitrage condition.
In a long gamma position, we make money on the large moves in the underlying and lose it on the small moves.
Gamma also plays an important role when there is a mismatch between the market’s view of volatility and the actual volatility of the underlying.
Since gamma is a measure of sensitivity of the hedge ratio \(\Delta\) to the movement in the underlying, the hedging requirement can be decreased by a gamma-neutral strategy. This means buying or selling more options, not just the underlying.
Theta
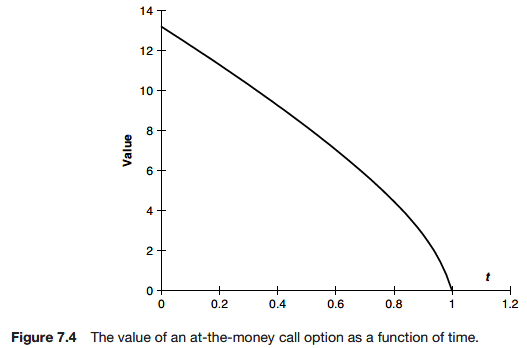
Theta is the rate of change of the option price with time
\[ \Theta = \frac{\partial V}{\partial t} \]
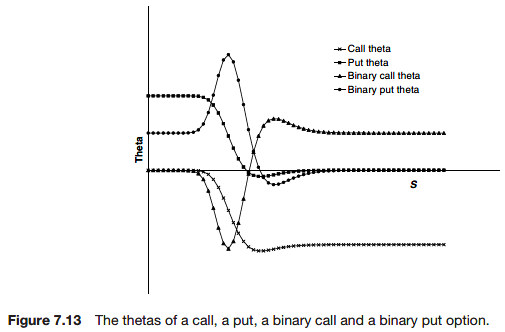
In a delta-hedged portfolio the theta contributes to ensuring that the portfolio earns the risk-free rate. But it contributes in a completely certain way, unlike the gamma which contributes the right amount on average.
Speed
The speed of an option is the rate of change of the gamma with respect to the stock price.
\[ Speed = \frac{\partial^3 V}{\partial S^3} \]
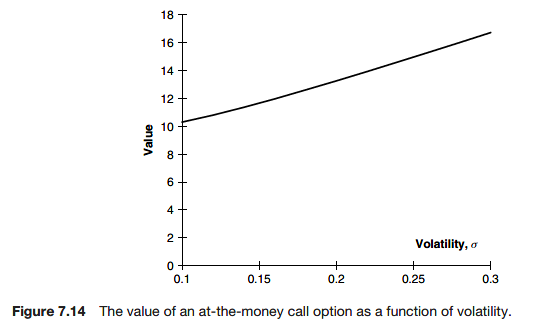
Vega
Vega, aka zeta and kappa, is a very important but confusing quantity. It is the sensitivity of the option price to volatility.
\[ Vega = \frac{\partial V}{\partial \sigma} \]
Vega is a derivative with respect to a parameter and not a variable.
As with gamma hedging, one can vega hedge to reduce sensitivity to the volatility.
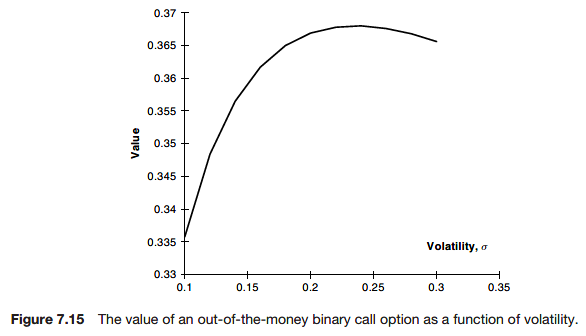
There is a downside to the measurement of vega. It is only really meaningful for options having single-signed gamma everywhere. call and put values (and options with single-signed gamma) have values that are monotonic in the volatility: increase the volatility in ca call and its value increases everywhere. Contracts with a gamma that changes sign may have a vega measured at zero because as we increase the volatility the price may rise somewhere and fall somewhere else. Such a contract is very exposed to volatility risk but that risk is not measured by the vega.
Rho
Rho is the sensitivity of the option value to the interest rate used in the Black-Scholes formulae:
\[ \rho = \frac{\partial V}{\partial r} \]
Rho would then be the sensitivity to the level of the rates assuming a parallel shift in rates at all times.
Implied volatility
If we can see the price at which the option is trading, we can ask ‘what volatility must I use to get the correct market price?’ This is called the implied volatility. The implied volatility is the volatility of the underlying which when substituted into the Black-Scholes formula gives a theoretical price equal to the market price. In a sense it is the market’s view of volatility over the life of the option.
Newton-Raphson uses the derivative of the option price with respect to the volatility (the vega) in the calculation.
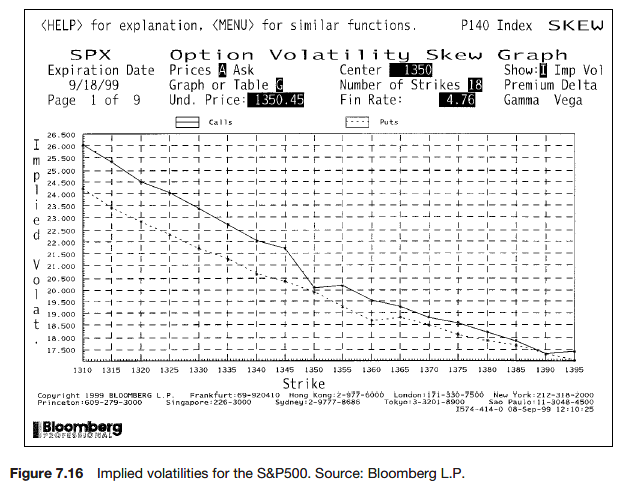
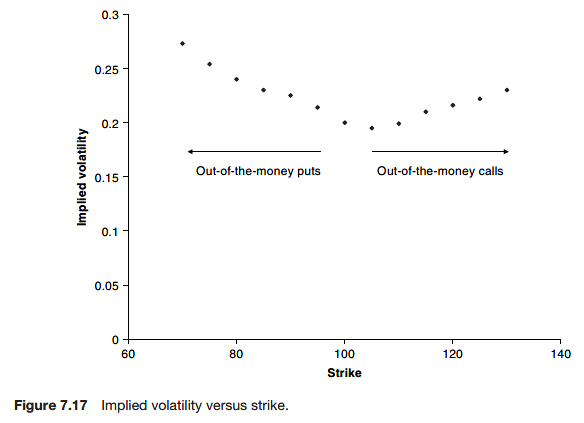
In practice if we calculate the implied volatility for many different strikes and expiries on the same underlying then we find that the volatility is not constant.
The implied volatilities for the calls and puts should be identical, because of put-call parity. The differences seen here could be due to bid-offer spread or calculations performed at slightly different times.
This shape is commonly referred to as the skew, or the smile, if it is turned up at both ends, but it could also be in the shape of a frown.
frown
- A frown is a facial expression in which the eyebrows are brought together, and the forehead is wrinkled, usually indicating displeasure, sadness or worry, or less often confusion or concentration
Implied volatility interpretation
- market view of future volatility
- uncertainty in volatility
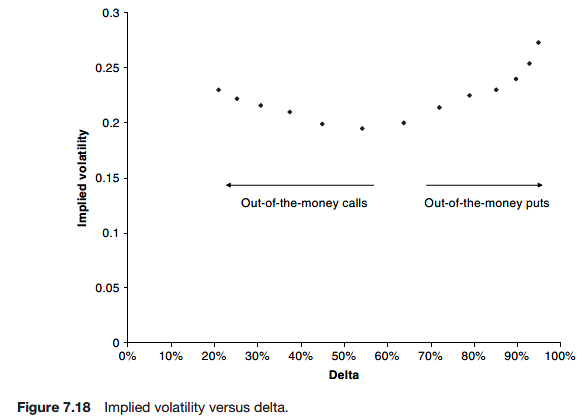
The important point is that in equity markets it is usually said that implied volatility stays unchanged as a function of strike whereas in FX markets the implied volatilities stay unchanged as a function of delta. These are called the sticky strike and sticky delta models.
A classification of hedging types
Why hedge?
Hedging in its broadest sense means the reduction of risk by exploiting relationships or correlation between various risky investments (or bets)
The two main classification
Model independent hedging
ex) put-call parity, spot-forward parity
Model-dependent hedging
If the model is wrong, then any hedging strategy will also be wrong.
Delta hedging
theoretically perfect elimination of all risk by delta hedging exploiting the perfect correlation between the changes in the option value and the stock price. → dynamic hedging
- continually monitored and frequently adjusted by the sale or purchase of the underlying asset.
Gamma hedging
To reduce the size of each rehedge and/or to increase the time between rehedges, and thus reduce costs, the technique of gamma hedging is often employed.
Gamma hedging is a more accurate form of hedging that theoretically eliminates these second-order effects.
Vega hedging
Vega hedge means that we hedge one option with both the underlying and another option in such a way that both the delta and the vega, the sensitivity of the portfolio value to volatility, are zero.
The distinction between variables (underlying asset price and time) and parameters (volatility, dividend yield, interest rate) is extremely important here. It is justifiable to rely on sensitivities of prices to variables, but usually not sensitivity to parameters. To get around this problem it is possible to model independently volatility etc. as variables themselves. In such a way it is possible to build up a consistent theory.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1116021/
Variables are quantities which vary from individual to individual. By contrast, parameters do not relate to actual measurements or attributes but to quantities defining a theoretical model.
https://s-nam.github.io/docs/academic_writing/word/2021-08-03-Parameter.html
Variable
- 보통 variable 은 어떤 함수 안에서 고정되지 않은 수를 말한다.
Parameter
- 한국어로는 ‘보조변수’, ‘매개변수’
- 변수와 관계가 있으나 아직 정해지지 않은, 실험을 통하여 정해지는 수
https://www.differencebetween.com/difference-between-variable-and-vs-parameter/
A variable is an entity that changes with respect to another entity. A parameter is an entity which is used to connect variables.
A variable is an entity which changes in a given system.
A parameter is an entity that is used to connect or unify two or more variables of an equation.
Static hedging
In practice, hedging must be done at discrete times and is costly. On theoretical side, the model for the underlying is not perfect, at the very least we do not know parameter values accurately. Delta hedging is exposed to model risk. This is eliminated by static hedging as well as delta hedging.
Static hedging is to buy or sell more liquid traded contracts to reduce the cashflows in the original contract. The static hedge is put into place now, and left until expiry.
Margin hedging
Often what causes banks, and other institutions, to suffer during volatile markets is not the change in the paper value of their assets but the requirement to come up suddenly with a large amount of cash to cover an unexpected margin call.
To cover the risk of default in the event of an unfavorable outcome, the clearing houses the register and settle options insist on the deposit of a margin by the writers of options.
- initial margin, maintenance margin
A dramatic market move could result in a sudden large margin call that may be difficult to meet. To prevent this situation it is possible to margin hedge. That is, set up a portfolio such that margin calls on one part of the portfolio are balanced by refunds from other parts. Usually over-the-counter contracts have no associated margin requirements and so won’t appear in the calculation.
Crash (Platinum) hedging
Market Crashes have at least two obvious effects on hedging
- The moves are so large and rapid that they cannot be traditionally delta hedged. The convexity effect is not small.
- Normal market correlations become meaningless. Typically all correlations become one (or minus one)
Crash or Platinum hedging exploits the latter effect in such a way as to minimize the worst possible outcome for the portfolio. Platinum hedging comes in two types:
- hedging the paper value of the portfolio
- hedging the margin calls
Further reading
