
- the meaning of early exercise
- the difference between European, American and Bermudan options
- how to value American options in the partial differential equation framework
- how to decide when to exercise early
- early exercise and dividends
Introduction
American options are contracts that may be exercised early, prior to expiry.
Most traded stock and futures options are American style, but most index options are European.
The perpetual American put
This contract can be exercised for a put payoff at any time. There is no expiry, that’s why it is called a ‘perpetual’ option.
The payoff is
The solution of the option is independent of time. It depends only on the level of the underlying.
When it comes to the general non-perpetual option, American option loses this property.
All American option can never go below the early-exercise payoff because of time value.
The perpetual option value is independent of t
The general solution of this second-order ordinary differential equation is
where A and B are arbitrary constants.
Suppose that the option is exercised at S = S*
for S > S*
This choice maximizes V(S) for all S ≥ S. The solution with this choice for S and with the corresponding B given by
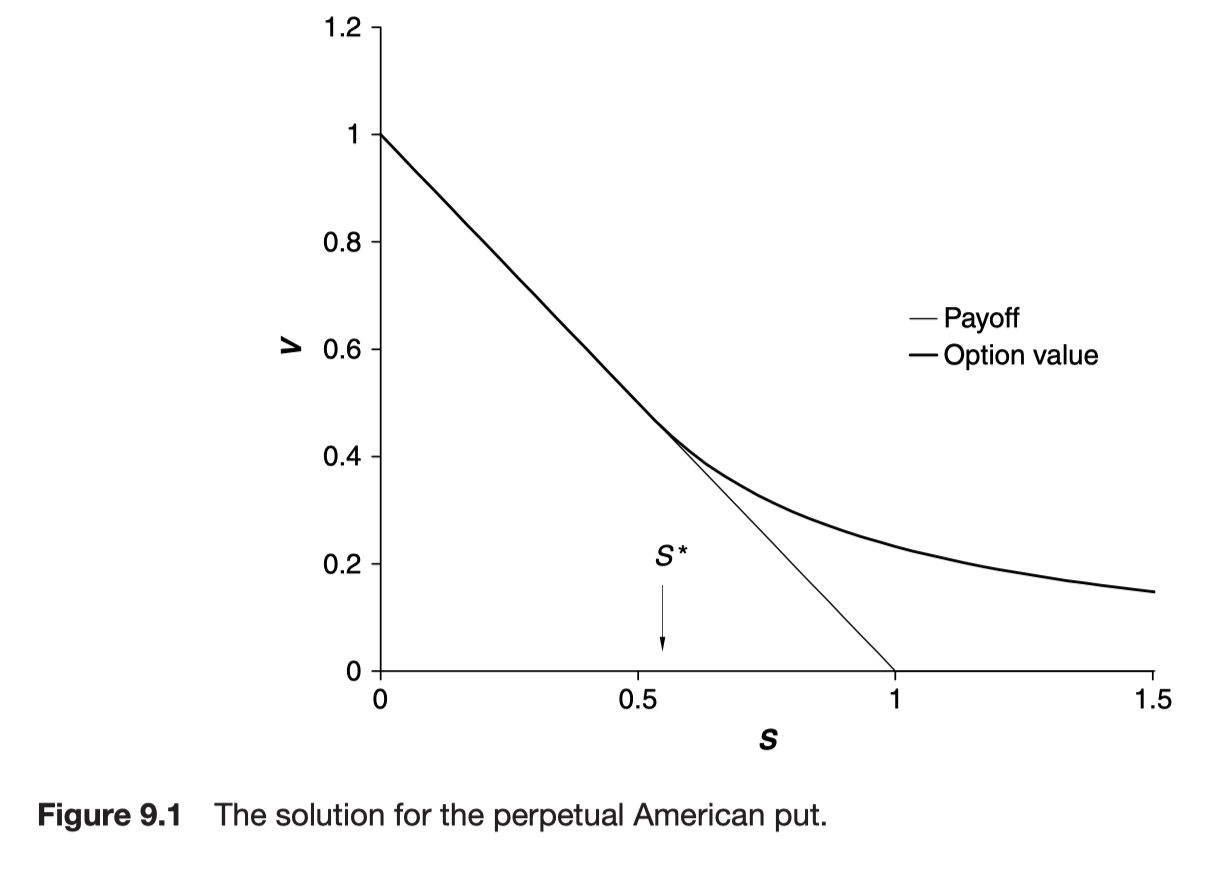
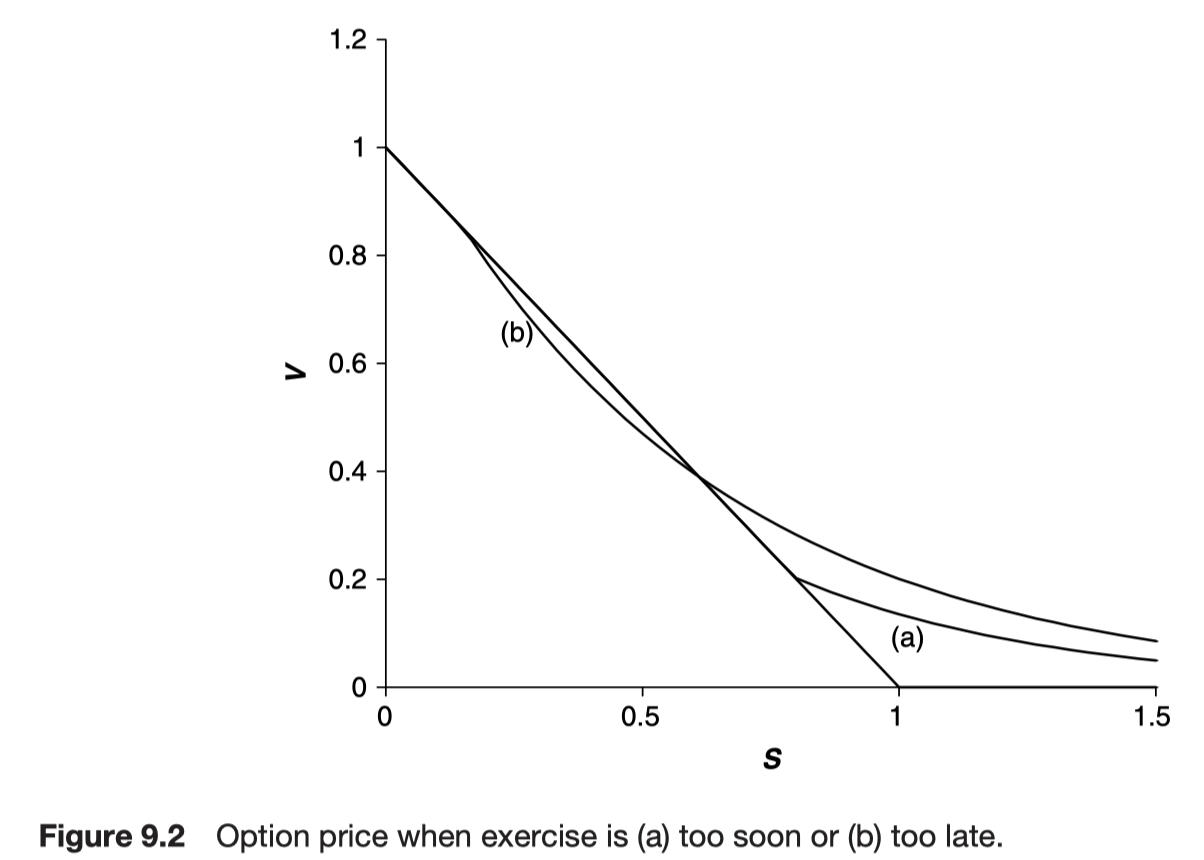
The slope of option value and the slope of the payoff function are the same at S = S*
High-contrast or smooth-pasting condition
- The American option value is maximized by an exercise strategy that makes the option value and option delta continuous
S* is called the optimal exercise point
When there is a continuous paid and constant dividend yield on the asset
The general solution is
Perpetual American put is
It is optimal to exercise when S reaches the value
Perpetual American call with dividends
The solution for the American perpetual call is
It is optimal to exercise S reaches
When D = 0, the solution is V = S, and S* becomes infinite. Thus, it is never optimal to exercise the American perpetual call. Its value is the same as the underlying.
Mathematical formulation for general payoff
Construct a portfolio of one American option with value V(S, t) and short a number
When the contract is American the long/short relationship is asymmetrical, it is the holder of the exercise rights who controls the early exercise feature.
If V is the value of long position in an American option, there is no more than the risk-free rate
Writer of the American option can make more than the risk-free rate
- if the holder does not exercise optimally.
- if the holder has a poor estimate of the volatility of the underlying
If the payoff for early exercise is P(S, t), possibly time-dependent, then the no-arbitrage constraint
At expiry
The option value is maximized if the owner of the option exercise such that
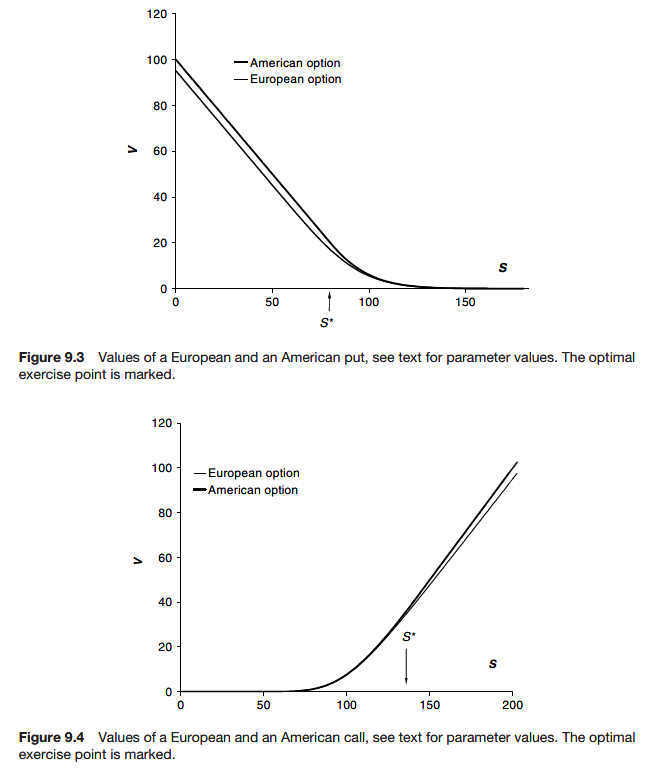
The value of American call option is the same as the value of European call option when the underlying pays no dividends.
Since the call option has a value which approaches
The problem for the American option is what is known as a free boundary problem. In the European option problem we know that we must solve for all values of S from zero to infinity. When the option is American we do not know a priori where the Black-Scholes equation is to be satisfied; this must be found as part of the solution. This means that we do not know the position of the early exercise boundary. Moreover, except in special and trivial cases, this position is time-dependent.
American option problem
- free boundary problem - do not know where the optimal position to exercise for American call option
- non-linear - cannot combine two separate solutions into one
With the perpetual American straddle, as defined here, one should exercise either if the asset gets too low or too high. The exact positions of the boundaries can be determined by making the option and its delta everywhere continuous.
Local solution for call with constant dividend yield
non-trivial problems → only can find local solutions, good approximation for some values of the assets at some times
When there is a long time to expiry and close to expiry, optimal exercise boundary for the American call option (r > D)
The call should be exercised if the asset rises above this value.
As
If the asset value rises above the free boundary it is better to exercise the option to receive the dividends than no continue holding it.
Near the point t = T, S = Er/D the option price is approximately
where
When D = 0, there is no free boundary → it is never optimal to exercise early
When r < D, the free boundary starts from S = E at time t = T.
Other dividend structures
Discrete paid dividend
The jump condition
Even though there is the jump condition derived from discrete dividend, this ensures that the realized option value is continuous.
The jump condition
This does not matter because continuity is only lost if one should have already optimally exercised before the dividend is paid.
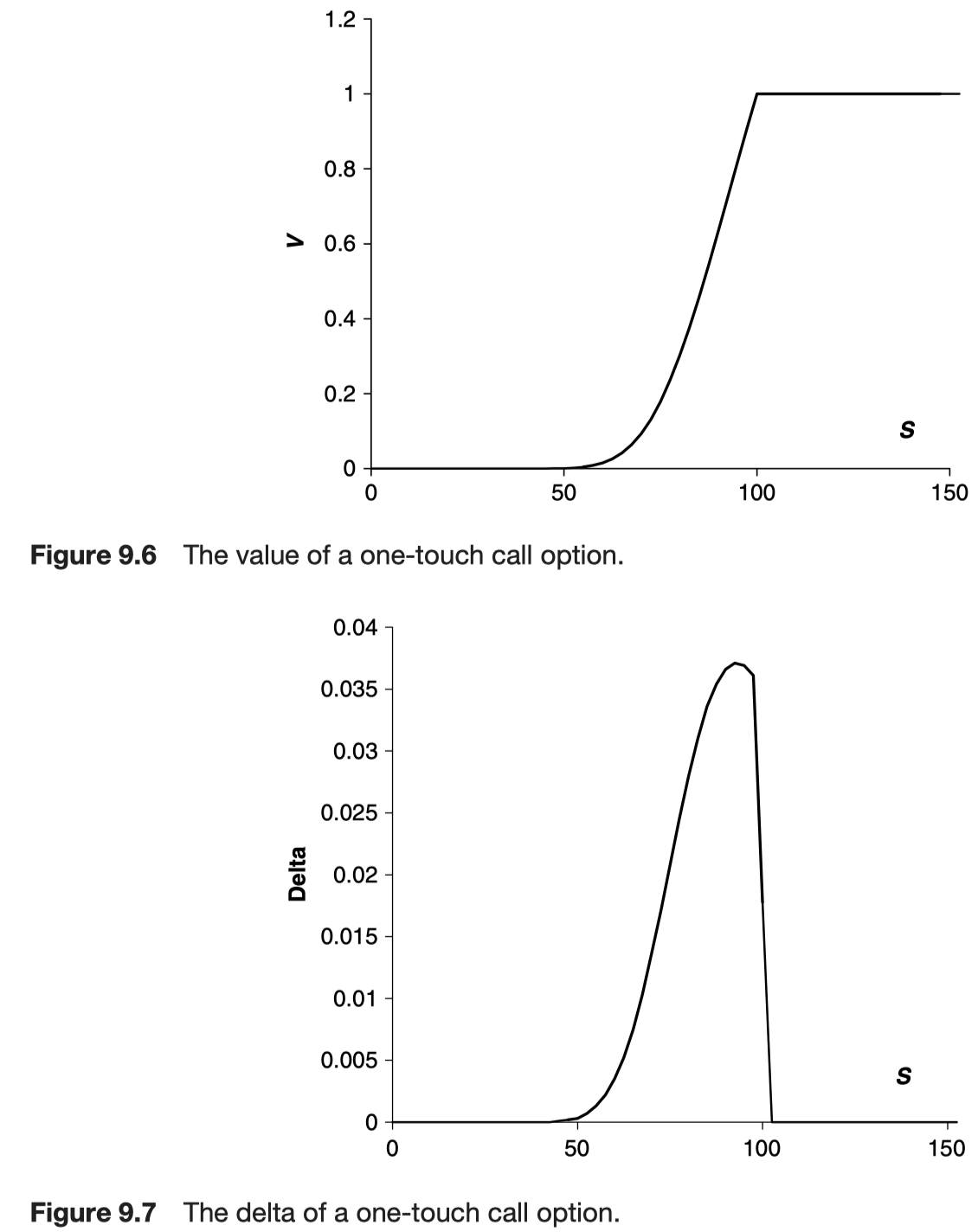
One-touch options
binary call/put for American option version
‘one touch’ means there is no benefit in holding the option once the level has been reached therefore it should be exercised immediately the level is reached for the first time.
For American option, optional exercise point must be decided.
For a one-touch call
When S less than
For one-touch put
The double one-touch option has both an upper and a lower level on which the payoff of $1 is received.
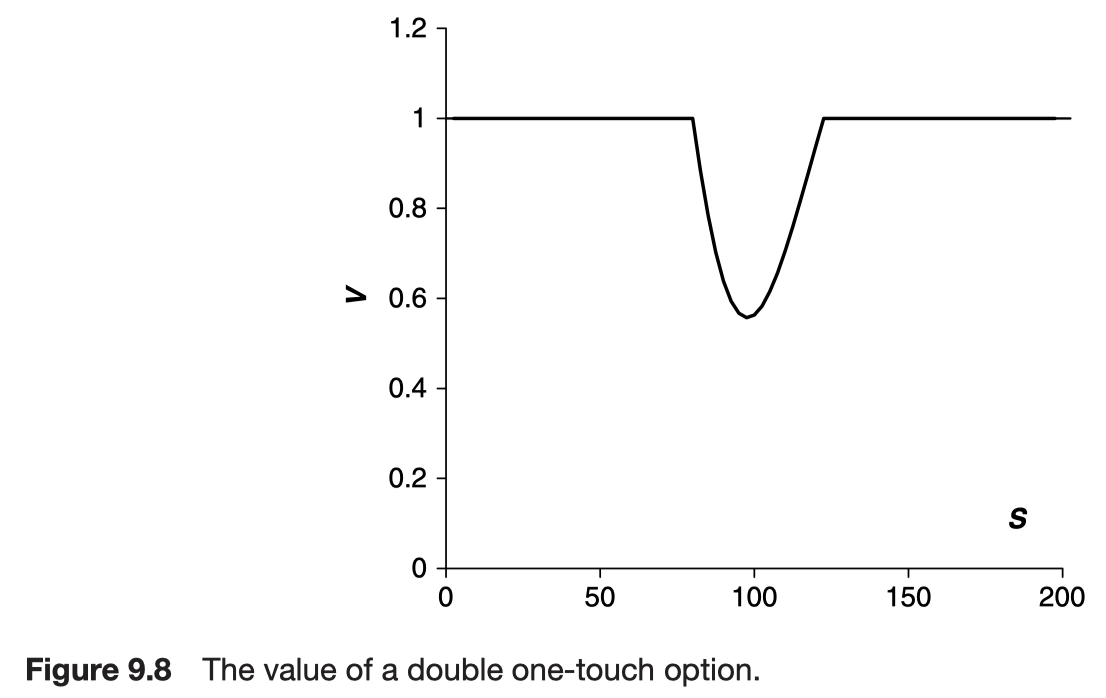
Other features in American-style contracts
Bermudan options
An option with such intermittent exercise opportunities is called a Bermudan option.
When the exercise dates on a second asset, the pricing Bermudan option is more complicated. (multi-asset contract)
Other issues
Non-linearity
The pricing of American option is a non-linear problem because of the free boundary.
Mathematically harder to solve than linear problem
Free-boundary problems
An example of a free-boundary option is the installment option. In this contract the owner must keep paying a premium, on prescribed dates, to keep the contract alive. If the premium is not paid then the contract lapses.
Part of the valuation is to decide whether or not it is worth paying the premium, or whether the contract should be allowed to lapse.
Continuous payment of a premium
If we impose the constraint
with continuity of the delta, and let the contract lapse if ever V = 0 then we give our contract the highest value possible.
Discrete payment case
- The value of the contract must increase in value from before the premium is paid to just after it is paid.
the jump condition
In practice, the premium L is chosen so that the value of the contract at initiation is exactly equal to L. This means that the start date is just like any other payment date.
Numerical solution
- binomial method
- Monte Carlo simulation
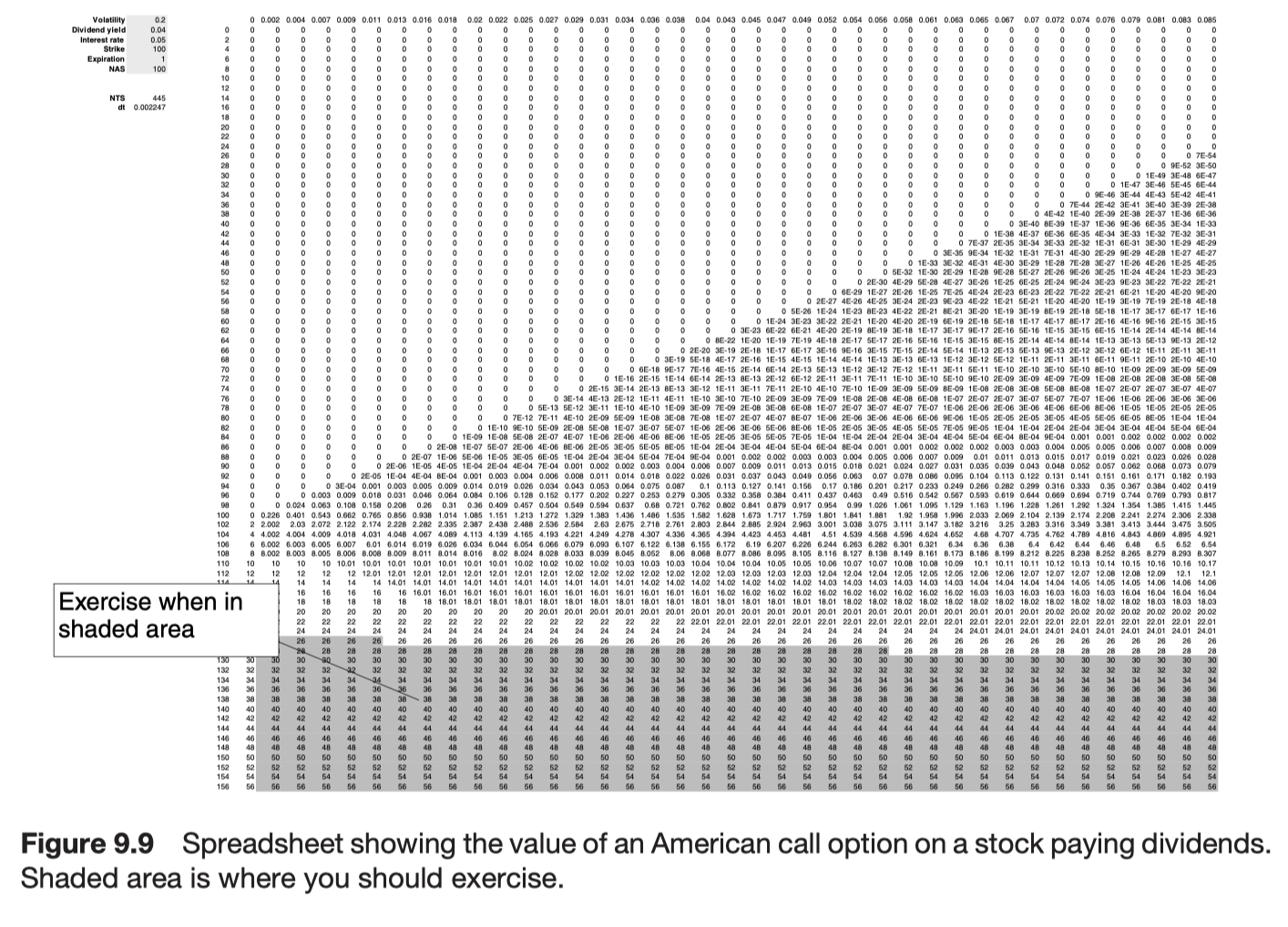
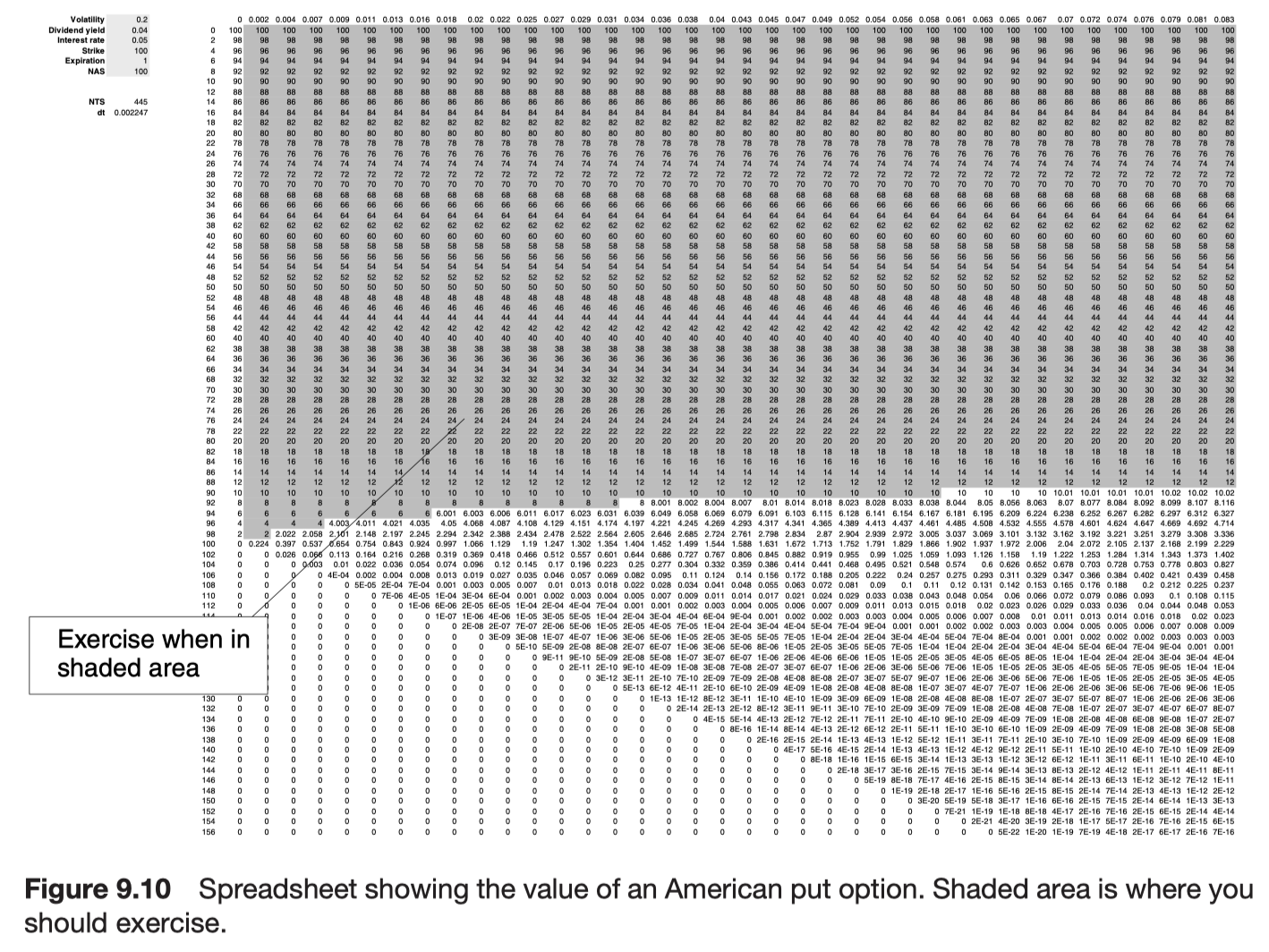
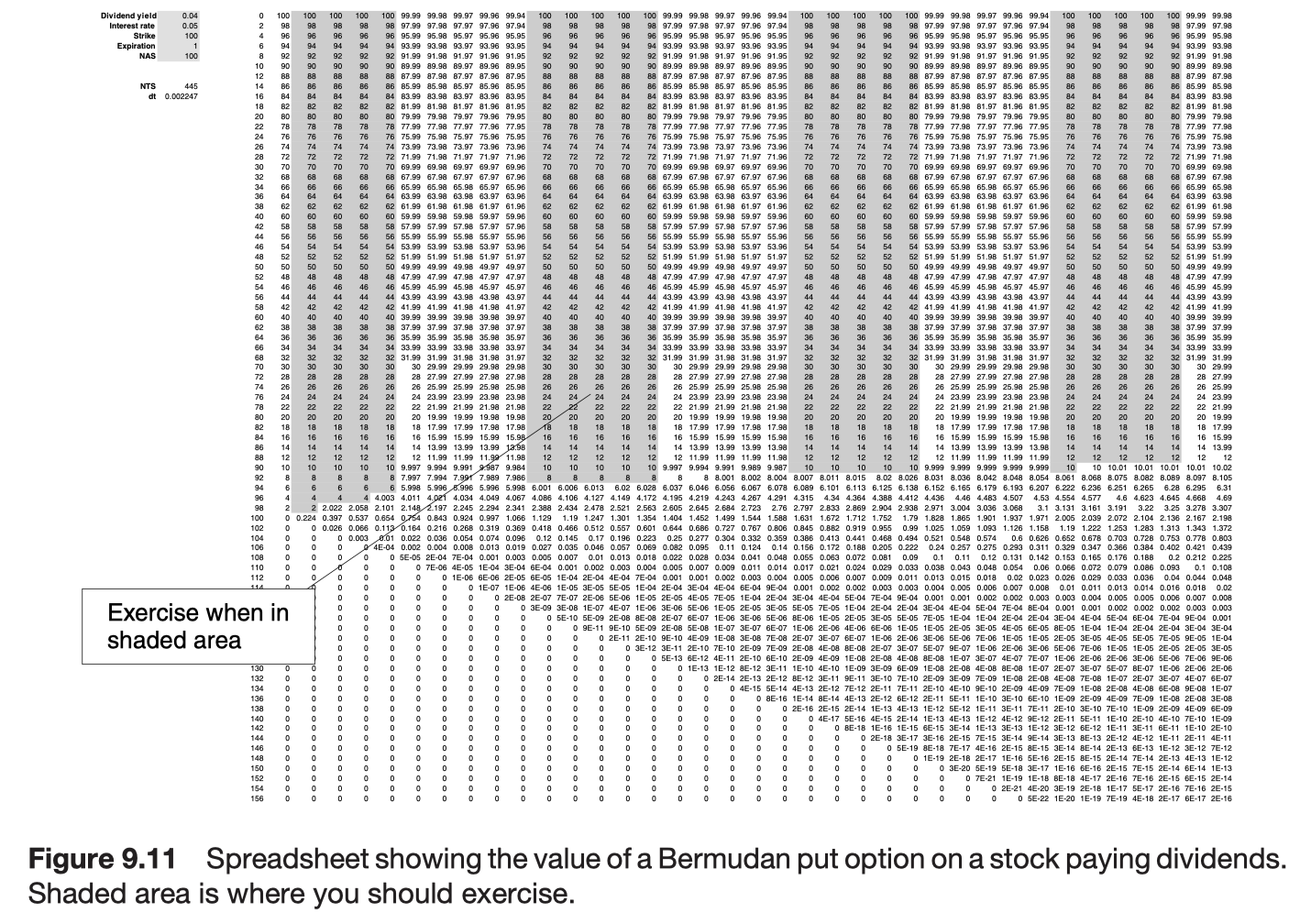
Further reading
