- the specifications of basic interest rate swap contracts
- the relationship between swaps and zero-coupon bonds
- exotic swaps
Introduction
A swap is an agreement between 2 parties to exchange, or swap, future cashflows. The size of these cashflow is determined by some formulae, decided upon at the initiation of the contract. The swaps may be in a single currency or involve the exchange of cashflows in different currencies.
The vanilla interest rate swap
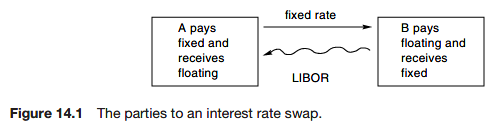
In the interest rate swap the 2 parties exchange cashflows that are represented by the interest on a notional principal. Typically, one side agrees to pay the other a fixed interest rate and the cashflow in the opposite direction is a floating rate.
One of the commonest floating rates used in a swap agreement is LIBOR.
At the maturity of the contract the principal is not exchanged.
Example
Every six months there is an exchange of such payments, with the fixed leg always being known and the floating leg being known six months before it is paid.
There is also the LIBOR in arrears swap in which the LIBOR rate paid on the swap date in the six-month rate set that day, not the rate set six months before.
Comparative advantage
Swaps were first created to exploit comparative advantage. This is when 2 companies who want to borrow money are quoted fixed and floating rates such that by exchanging payments between themselves they benefit, at the same time benefitting the intermediary who puts the deal together.
\[ LIBOR + 30bps + 8.2\% = LIBOR + 8.5\% \]
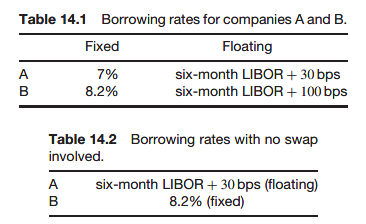
- fixed payer: B
- floating payer: A
\[ LIBOR + 100bps + 7\% = LIBOR + 8\% \]
- fixed payer: A
- floating payer: B
That’s a saving of 5%.
Although comparative advantage was the original reason for the growth of the swaps market, it is no longer the reason for the popularity of swaps.
- swap을 bond portfolio로 볼 수 있고, bond는 모든 상품이 모든 시점에 대응하는 상품이 존재하지 않음. 따라서 vanila swap이 more liquid해졌고, 과거에는 bond로 swap을 pricing했는데, 이제는 swap으로 bond를 pricing하는 때가 왔다고 이해할 수 있음
The swap curve
The present value of the fixed side and the floating side both have the same value, netting out to zero.
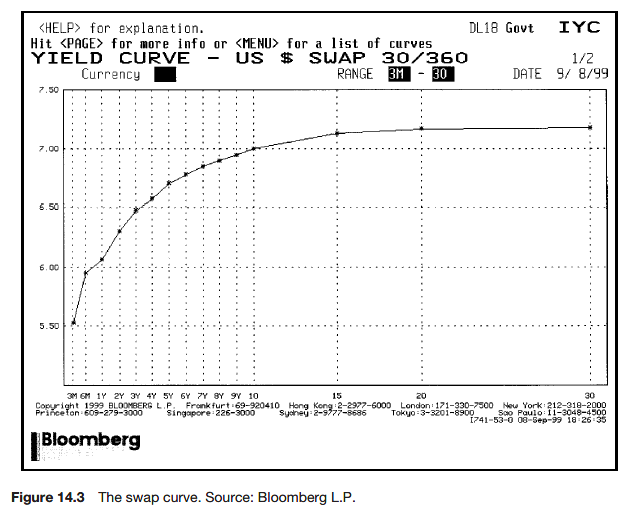
The swaps market is so liquid, at so many maturities. The fixed leg of a par swap (having no value) is determined by the market.
The rates of interest in the fixed leg of a swap are quoted at various maturities. These rates make up the swap curve.
One way is to observe that a swap can be decomposed into a portfolio of bonds and so its value is not open to question if we are given the yield curve.
Relationship between swaps and bonds
If the fixed rate of interest is \(r_s\) and the time between payments is \(\tau\) then the fixed payments add up to
\[ r_s\tau\sum_{i = 1}^N{Z(t; T_i)} \]
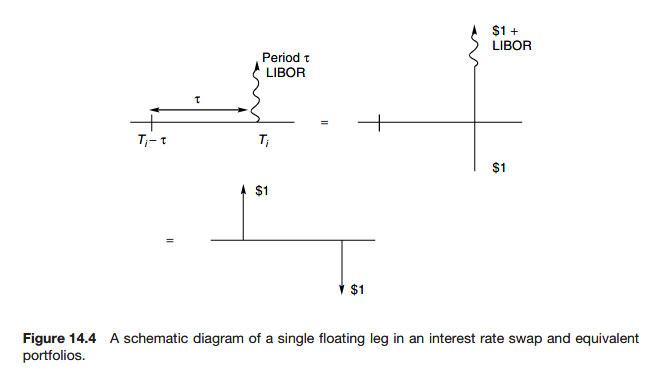
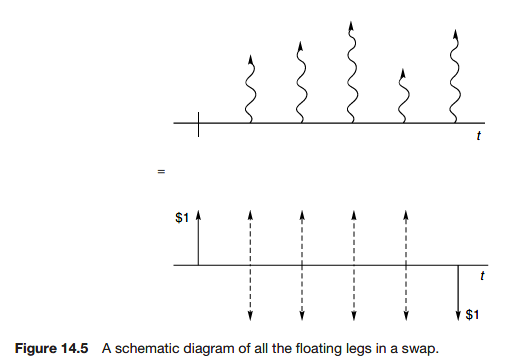
Bring the fixed and floating sides together to find that the value of the swap, to the receiver of the fixed side, is
\[ r_s\tau \sum_{i = 1}^N{Z(t; T_i)} - 1 + Z(t; T_N) \]
The result is model independent. This relationship is independent of any mathematical model for bonds or swaps.
At the start of the swap contract the rate \(r_s\) is usually chosen to give the contract par value
\[ r_s = \frac{1 - Z(t; T_N)}{\tau \sum_{i = 1}^N{Z(t; T_i)}} \]
This is the quoted swap rate.
Bootstrapping
\[ Z(t; T_1) = \frac{1}{1 + r_s(T_1)\tau} \]
\[ Z(t; T_{j + 1}) = \frac{1 - r_s(T_{j + 1})\tau\sum_{i = 1}^N{Z(t; T_i)}}{1 + r_s(T_{j + 1})\tau} \]
Other features of swaps contracts
Callable and puttable swaps
A callable or puttable swap allows one side or the other to close out the swap at some time before its natural maturity.
Extendible swaps
The holder of an extendible swap can extend the maturity of a vanilla swap at the original swap rate.
Index amortizing rate swaps
The principal in the vanilla swap is constant. In some swaps the principal declines with time according to a prescribed schedule. The index amortizing rate swap is more complicated still with the amortization depending on the level of some index, say LIBOR, at the time of the exchange of payments.
Other types of swap
Basis rate swap
In the basis rate swap the floating legs of the swap are defined in terms of two distinct interest rates. Basis risk can be reduced with a suitable basis rate swap.
Equity swaps
The basic equity swap is an agreement to exchange two payments, one being an agreed interest rate (either fixed or floating) and the other depending on an equity index.
The equity basis swap is an exchange of payments based on two different indices.
Currency swaps
A currency swap is an exchange of interest payments in one currency for payments in another currency. The interest rates can both be fixed, both floating or one of each. As well as the exchange of interest payments there is also an exchange of the principals (in two different currencies) at the beginning of the contract and at the end.
Further reading
