
- the rules of blackjack
- blackjack strategy and card counting
- the Kelly criterion and money management
- no arbitrage in horse racing
The rules of blackjack
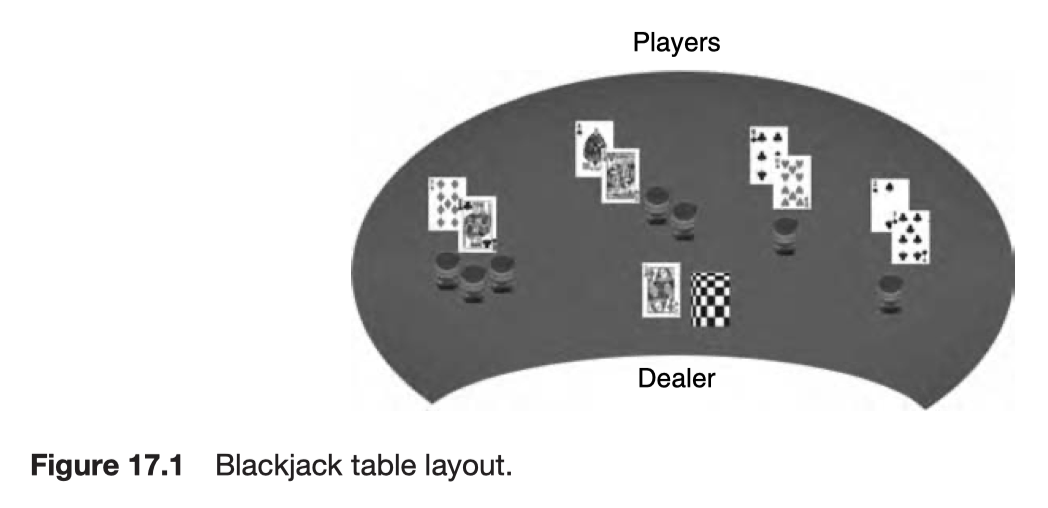
The aim of the game for the player is to hold a card count greater than that of the dealer without exceeding 21 (going ‘bust’)
Kings, queens and jacks: 10
ace: 11
all other cards: face value
- The player must place his bet in front of his table position
- The dealer deals 2 cards to each of the players, and 2 to himself
- One of the dealer’s cards dealt face up and the other face down
- If the player’s first 2 cards are an Ace and a 10-count card → blackjack or a natural → the player wins unless the dealer also has a natural
- the case of dealer’s natural - push → no money changes
- The dealer asks each player whether they want to hit or stand or doubling down
- hit: draw another card
- stand: no more cards are taken
- doubling down: double the bet on his first 2 cards and draw 1 additional card only
- If the player hits and bursts, his wager is lost
- The player can keep taking cards until he is satisfied with his count or busts
- splitting pairs: If the first 2 cards a player is dealt are a pair, he may split them into 2 separate hands, bet the same amount on each and then play them as 2 distinct hands
- Aces can receive only 1 additional card
- After splitting, Ace + 10 counts as 21 and not as blackjack.
- If the dealer’s up card is an ace, the player may take insurance, a bet not exceeding one half of his original bet.
- If the dealer’s down card is a 10-count card, the player wins 2 to 1. Any other card means a win for the dealer.
- In a time no money is won or lost, but the bets stays on the table for the next round
The dealer has no decisions to make. He must always follow very simple rules when it comes to hitting or standing. He must draw on 16 and stand on 17. In some casinos, the dealer is required to draw on soft 17 (a hand in which an ace counts as 11, not one). Regardless of the total the player has, the dealer must play this way.
The advantage to the dealer is that the player can go bust, losing his bet immediately, even if the dealer later busts. The asymmetry is the key to the house’s edge. The key to the player’s edge, which we will be exploiting shortly, is that he can vary both his bets and his strategy.
Beating the dealer
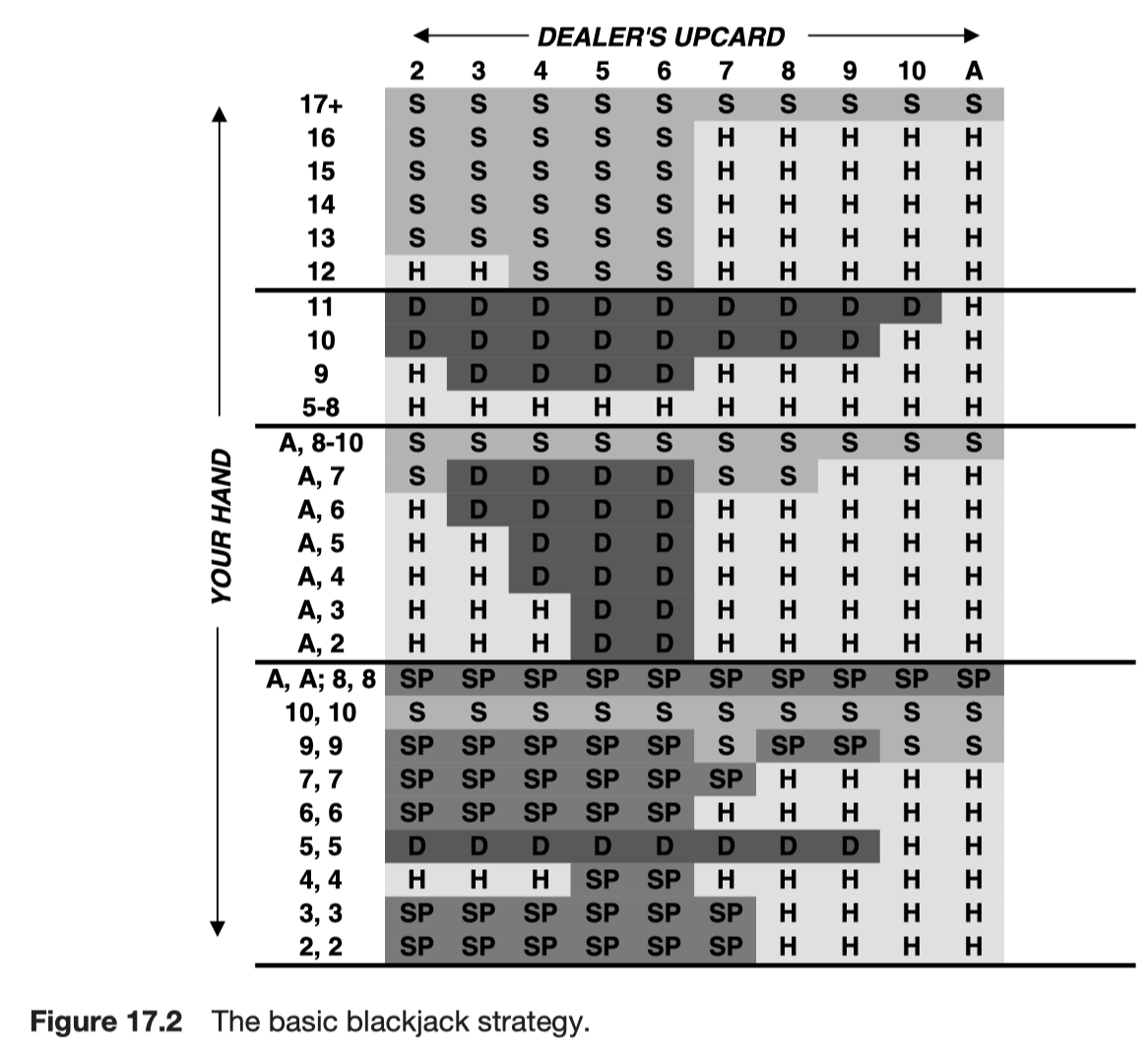
Keys to success in blackjack
- having the optimal strategy
- card counting
card counting is a technique to calculate approximate percentage of cards remaining in the deck. Blackjack has memory. During one hand depends on the previous hands and the cards that have already been dealt out.
With a fresh deck(s) start from zero, and then for every ace and 10 that is dealt subtract one; for every 1-6 add one. The larger the count, divided by an estimate of the number of cards left in the deck, the better are your changes of winning.
Ed Thorp combined the card counting idea, money management techniques (such as the Kelly criterion) and the optimal play strategy to devise a system that can be used by anyone to win at this casino game.
Summary of winning at blackjack
- If your strategy is to copy the dealer’s rules then there is a house edge of between 5 and 6 percent.
- The best strategy involves knowing when to hit or stand, when to split, double down, take insurance etc. This decision will be based on the 2 cards you hold and the dealer’s face up card. If you play the best strategy you can cut the odds down to about evens.
- To win at blackjack takes patience and the ability to count cards
- If you follow the optimal strategy and simultaneously bet high when the deck is favorable, and low otherwise, then you will win in the long run.
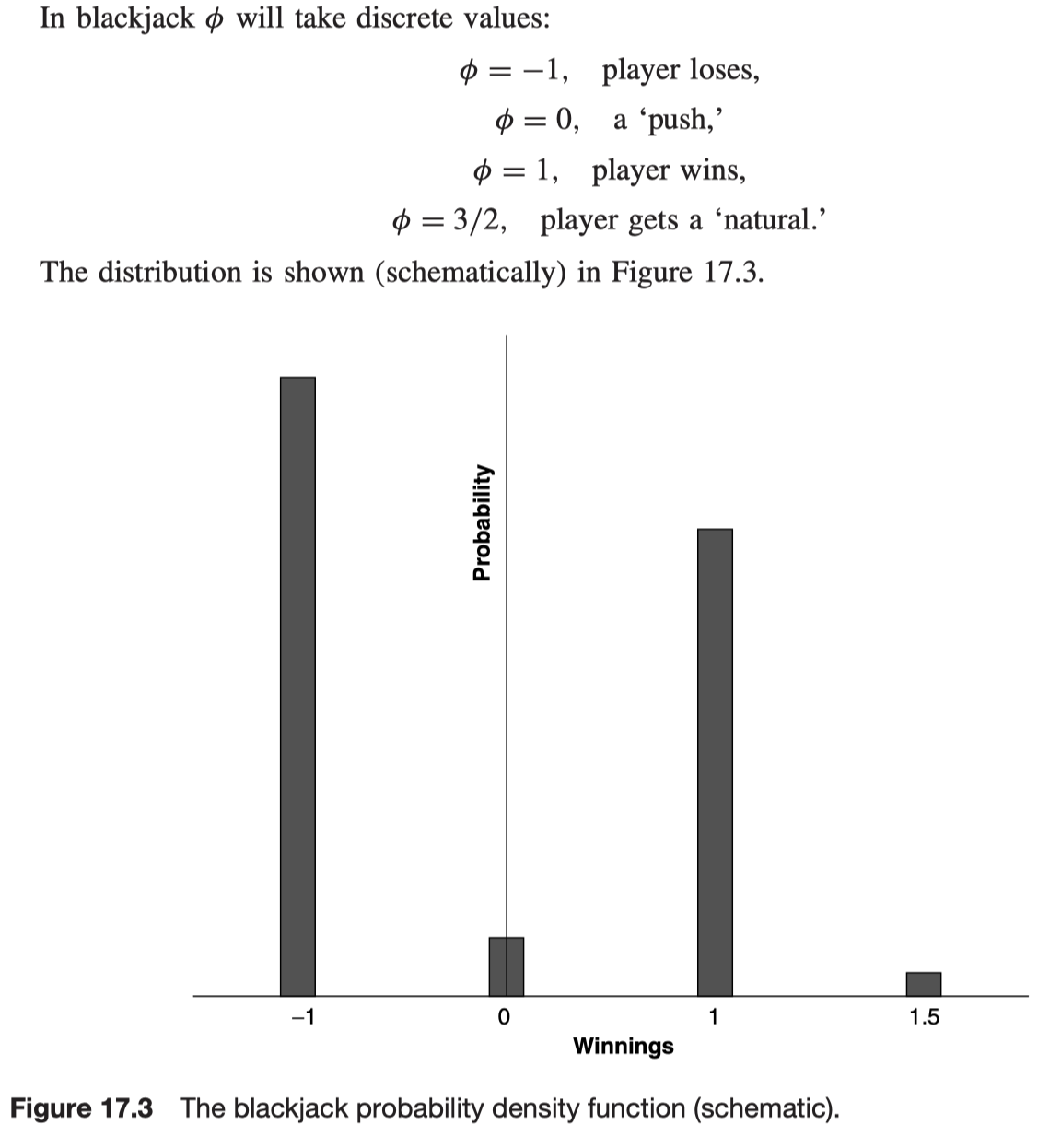
The distribution of profit in blackjack
The Kelly criterion

Kelly criterion is a very simple way to optimize your bets or investments so as to maximize your long-term average growth rate.
The fraction f is to maximize expected long-term growth rate.
This growth rate is given by
Assuming that the outcome of each hand is independent, then the expected value of this is
Expanding the argument of the logarithm in Taylor series, we get
Now assuming that the mean is small but that the standard deviation is not, we find that the expected long-term growth rate is approximately
This is maximized by the choice
giving an expected growth rate of
per hand.
If Kelly criterion.
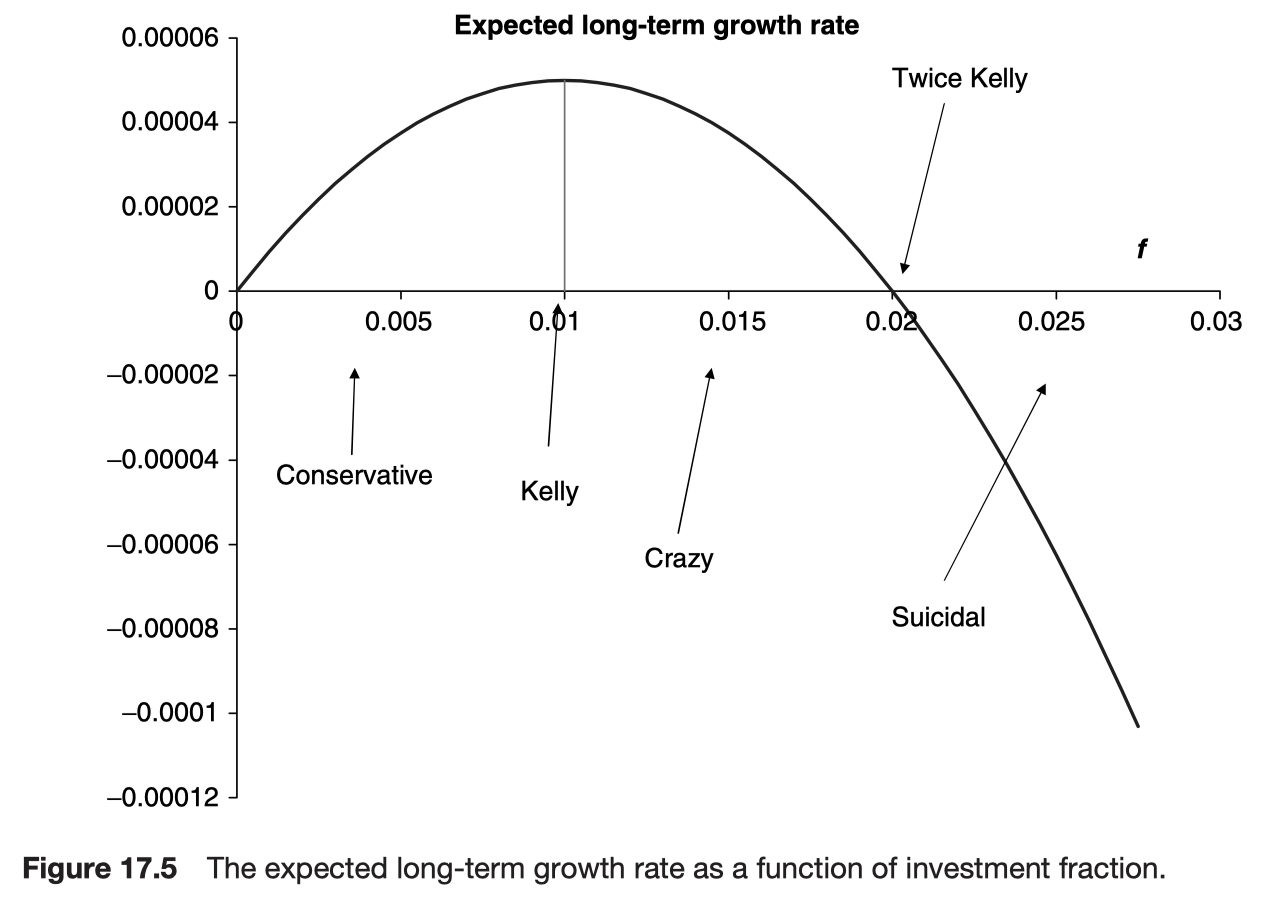
Given that in practice you rarely know the odds accurately it makes sense to bet conservatively, in case you accidentally stray into the crazy zone. For that reason many people use ‘half Kelly’ that is a fraction that is half of the Kelly fraction.
If you can play M times in an evening you would expect a total growth of
using full Kelly.
The Kelly criterion is about maximizing expected long-term growth. There are many other quantities to optimize, of course, so the Kelly criterion might not be the right choice for you.
Horse race betting and no arbitrage
The value of an option can be interpreted as the present value of the expected payoff, with the expectation being with respect to the risk-neutral asset price path. In this context risk neutral just means that the asset price increases with a growth rate that is the same as the risk-free interest rate. In other words, what we really believe that the asset price is going to do in the future (in terms of its growth rate) is irrelevant. We don’t even need to know the growth rate of an asset to price its options, only its volatility.
Setting the odds in a sporting game
Depending on how the betting goes, the odds will be set so that the house/bookie cannot lose.
Therefore it’s unlikely for there to be a sure-fire bet (unless the bookie has made a mistake, the race is fixed, or you can find 2 or more bookies that aren’t directly or indirectly laying off their bets on each other)
But you can win, on average. By exploiting the difference between the real probability of a horse winning and the odds you can get.
The mathematics
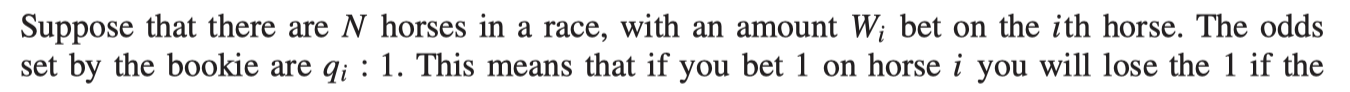

Arbitrage
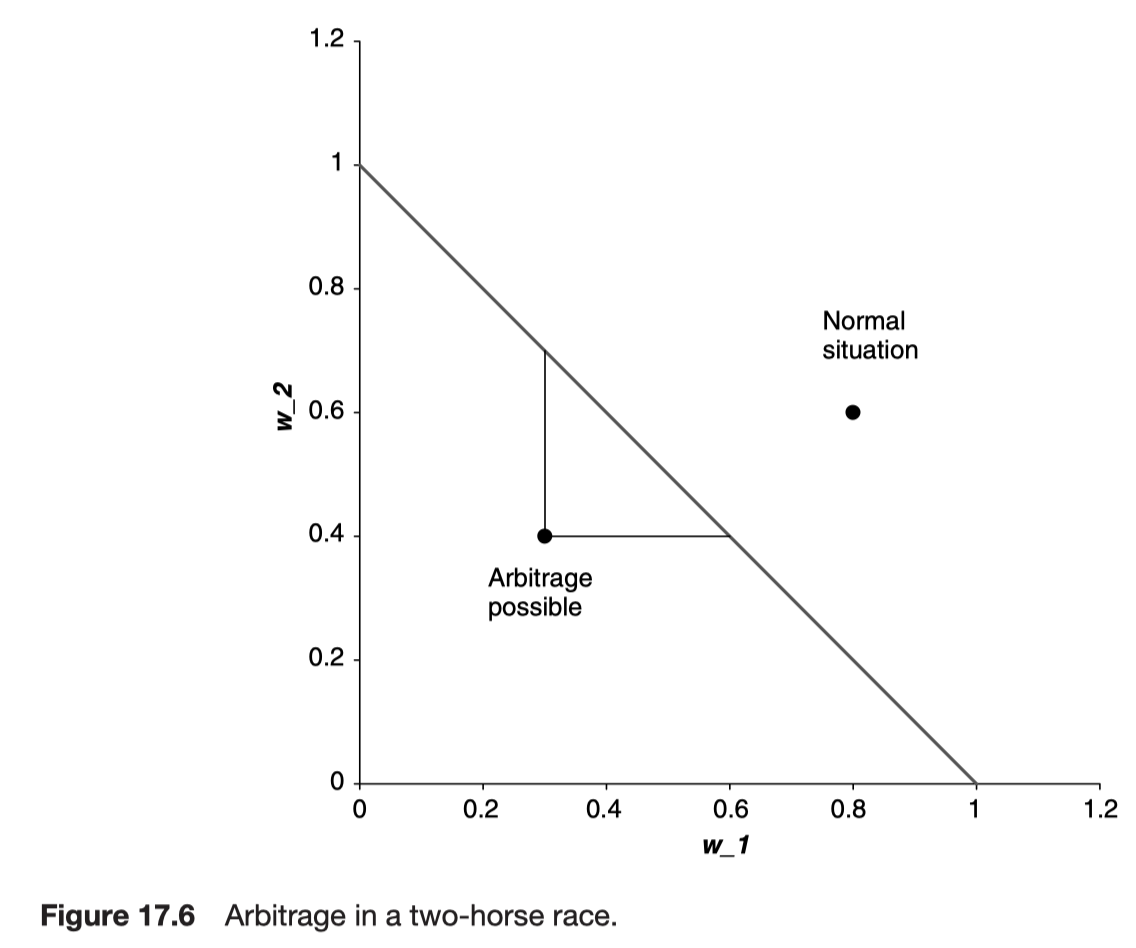
How best to profit from the opportunity?
There’s a simple test to see whether we are in an arbitrage situation. In general, if
the there is no arbitrage. If the sum is less than 1, there is an arbitrage.
You can benefit from the arbitrage by placing wagers
How to bet

This measures the dispersion of winnings about the average, and is often interpreted as a measure of risk. If this were zero our profit or loss would be a sure thing.
Scenario 1: maximize expected return
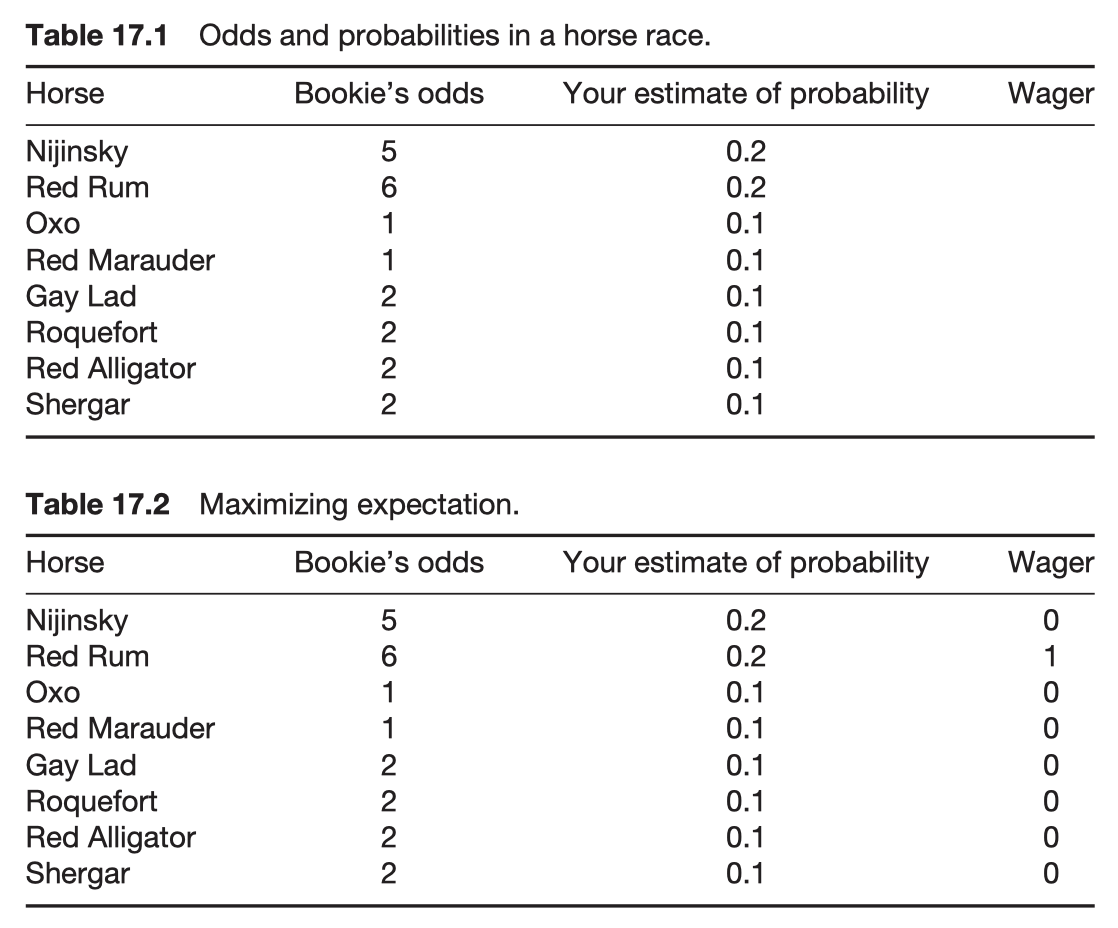
Scenario 2: minimize standard deviation
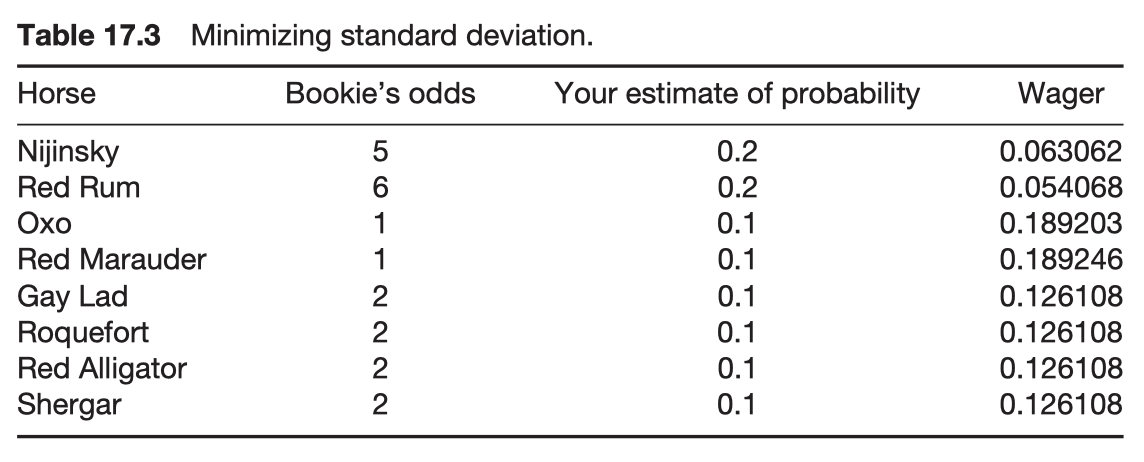
Scenario 3: maximize return divided by standard deviation

Further reading
